

Next: The Low-Energy Theory of
Up: PHYS 560: Lectures During
Previous: Chiral Symmetry and Isospin
Given the previous and somewhat technical discussion about QCD, lets look at
what we know exists in nature.
We know that the lightest spin
 strongly interacting particles
that can be made in the laboratory are the proton and neutron.
The proton has mass
strongly interacting particles
that can be made in the laboratory are the proton and neutron.
The proton has mass
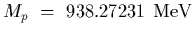 ,
and
,
and
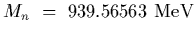 There are other properties that have been measured, and can be found in the
particle data group compilation[3].
There you can find, for the proton
There are other properties that have been measured, and can be found in the
particle data group compilation[3].
There you can find, for the proton
and for the neutron
Some comments:
- 1.
- The masses of the neutron and proton are very similar, differing at the
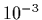 level.
Now, perhaps most fortunately for us, the neutron is slightly heavier than the
proton, so that
level.
Now, perhaps most fortunately for us, the neutron is slightly heavier than the
proton, so that
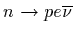 in free space, and not
in free space, and not
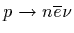 as would happen if
as would happen if 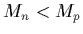 .
This scenario would mean that there is no stable hydrogen, and hence a very
different universe than the one we live in!
.
This scenario would mean that there is no stable hydrogen, and hence a very
different universe than the one we live in!
- 2.
- So far an electric dipole for neither the proton
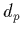 nor the neutron
nor the neutron 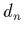 has been measured.
Such a quantity violates time-reversal invariance, a symmetry that we
expect to satisfied in nature to a very high precision.
However, the present limit on
has been measured.
Such a quantity violates time-reversal invariance, a symmetry that we
expect to satisfied in nature to a very high precision.
However, the present limit on 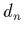 is close to where some extensions to the
standard model of electroweak interactions would may produce a value for
is close to where some extensions to the
standard model of electroweak interactions would may produce a value for 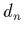 .
The standard model is estimated to give a
.
The standard model is estimated to give a 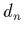 a few orders of magnitude lower.
a few orders of magnitude lower.
- 3.
- It is clear from the fact that both the neutron and proton have non-zero
charge radii (for a review see [4]) and also non-zero electric and
magnetic polarizabilities,
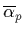 ,
,
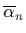 that the neutron and
proton are not point like objects, and have an extended size not so much
smaller than
that the neutron and
proton are not point like objects, and have an extended size not so much
smaller than
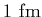 .
A plot of the proton charge form factor can be seen in fig. (2).
If the proton wa s apoint object then we would expect the curve to behave like
.
A plot of the proton charge form factor can be seen in fig. (2).
If the proton wa s apoint object then we would expect the curve to behave like
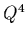 ,
which clearly it doesn't!
,
which clearly it doesn't!
Figure:
The proton charge form factor 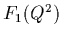 multiplied by
multiplied by 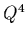 .
Data is from the E136 experiment at SLAC (reproduced without permission).
.
Data is from the E136 experiment at SLAC (reproduced without permission).
![\includegraphics[width=3in]{/home/savage/Teaching/Class560/Lec560_1/E136F1.ps}](img85.gif)
|


Next: The Low-Energy Theory of
Up: PHYS 560: Lectures During
Previous: Chiral Symmetry and Isospin
Martin Savage
1999-10-04
![]() strongly interacting particles
that can be made in the laboratory are the proton and neutron.
The proton has mass
strongly interacting particles
that can be made in the laboratory are the proton and neutron.
The proton has mass
![]() ,
and
,
and
![]() There are other properties that have been measured, and can be found in the
particle data group compilation[3].
There you can find, for the proton
There are other properties that have been measured, and can be found in the
particle data group compilation[3].
There you can find, for the proton
![\includegraphics[width=3in]{/home/savage/Teaching/Class560/Lec560_1/E136F1.ps}](img85.gif)