

Next: Protons and Neutrons
Up: A General Picture of
Previous: A General Picture of
Let us examine the part of
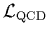 that describes the
that describes the 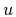 (up),
(up),
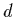 (down) quarks and gluons only in the limit of
(down) quarks and gluons only in the limit of
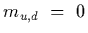 ,
,
This lagrange density is clearly invariant under the global transformations
| |
|
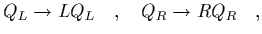 |
(4) |
where 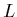 and
and 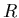 are independent SU(2) unitary transformation matrices,
are independent SU(2) unitary transformation matrices,
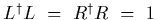 .
If we choose
.
If we choose 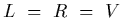 ,
this corresponds to transforming the left and right handed
fields by the same ``amount''.
If the world ``looked'' the same no matter what we choose for
,
this corresponds to transforming the left and right handed
fields by the same ``amount''.
If the world ``looked'' the same no matter what we choose for
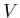 then we would say that the world was invariant under isospin
transformations (I will use
then we would say that the world was invariant under isospin
transformations (I will use 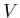 to denote the transformation in this
section. Be aware that I will change notation in the near future for ease).
In fact, isospin is found to be a very good symmetry of nature, that is to say
that the world only changes a little bit under isospin transformations.
to denote the transformation in this
section. Be aware that I will change notation in the near future for ease).
In fact, isospin is found to be a very good symmetry of nature, that is to say
that the world only changes a little bit under isospin transformations.
It turns out that when we consider the non-zero values of the quark masses
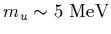 and
and
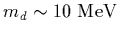 ,
isospin symmetry is
explicitly broken,
,
isospin symmetry is
explicitly broken,
with
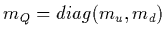 .
Given that the
.
Given that the 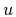 and
and 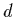 masses differ by a factor of two it might first
appear that isospin will be badly broken.
However this is not the case.
The typical scale for the size of hadronic interaction strengths is set by the
scale at which spontaneous symmetry breaking occurs, i.e. when
masses differ by a factor of two it might first
appear that isospin will be badly broken.
However this is not the case.
The typical scale for the size of hadronic interaction strengths is set by the
scale at which spontaneous symmetry breaking occurs, i.e. when
| |
|
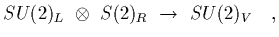 |
(6) |
due to 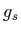 becoming large.
This scale is called the chiral symmetry breaking scale and is
becoming large.
This scale is called the chiral symmetry breaking scale and is
| |
|
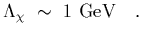 |
(7) |
Therefore, we conclude that the appropriate small dimensionless
parameter that describes
isospin breaking is
| |
|
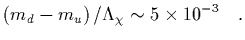 |
(8) |
Thus, isospin symmetry is an accidental symmetry of nature.
It is an accident because the scale of chiral symmetry breaking and the
mechanism that produces the quarks masses (the Higgs mechanism) are unrelated.


Next: Protons and Neutrons
Up: A General Picture of
Previous: A General Picture of
Martin Savage
1999-10-04
![]() that describes the
that describes the ![]() (up),
(up),
![]() (down) quarks and gluons only in the limit of
(down) quarks and gluons only in the limit of
![]() ,
,
![]() and
and
![]() ,
isospin symmetry is
explicitly broken,
,
isospin symmetry is
explicitly broken,