

Next: Isospin
Up: The Low-Energy Theory of
Previous: The Low-Energy Theory of
One of the implications of our understanding of QCD and the spontaneous
breaking of chiral symmetry, is that there should be a nearly massless
strongly interacting spin-zero particle, a pseudo-Goldstone particle.
When we say nearly massless, we mean that the mass is much less than typical
strong interaction length scales
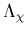 .
In the limit that the up and down quark masses were to vanish then this
particle would have exactly zero mass.
The pion (
.
In the limit that the up and down quark masses were to vanish then this
particle would have exactly zero mass.
The pion (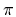 )
has been identified with this particle and it will play a
significant role in our discussions of nuclear physics.
There are three different charge states,
)
has been identified with this particle and it will play a
significant role in our discussions of nuclear physics.
There are three different charge states, 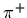 ,
,
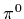 and the
and the 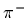 .
The properties of the
.
The properties of the 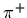 and
and 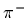 are identical by the CPT theorem
(Field Theory).
In [3] you will find
are identical by the CPT theorem
(Field Theory).
In [3] you will find
It is clear that the 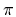 's are also very interesting objects.
In fact a large part of nuclear and hadronic physics has been spent better
understanding exactly what a pion is!
We will not really get into this area during this course, but may step toward
that during the next quarter.
's are also very interesting objects.
In fact a large part of nuclear and hadronic physics has been spent better
understanding exactly what a pion is!
We will not really get into this area during this course, but may step toward
that during the next quarter.


Next: Isospin
Up: The Low-Energy Theory of
Previous: The Low-Energy Theory of
Martin Savage
1999-10-04