In previous work, we showed that the long-distance part of the
potential between nucleons in partially-quenched QCD is very different
to that in QCD due to the contribution from hairpin interactions [15].
Such interactions give rise to an exponentially falling potential as opposed to
the Yukawa behavior that one finds in QCD. The coefficient of this
exponential component depends upon the difference between sea and valence quark
masses.
In our recent work we explore the scattering amplitudes directly in PQ![]() PT.
We find that calculations are straightforward with BBSvK power-counting, and we
were able to produce amplitudes in the
PT.
We find that calculations are straightforward with BBSvK power-counting, and we
were able to produce amplitudes in the
![]() channel and potentials that are to
be used in the Schrodinger equation in the
channel and potentials that are to
be used in the Schrodinger equation in the
![]() coupled-channels.
For instance the scattering volumes in the P-waves are
coupled-channels.
For instance the scattering volumes in the P-waves are
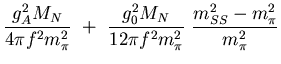 |
|||
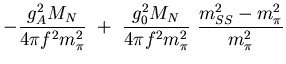 |
|||
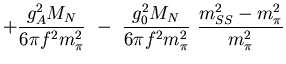 |
|||
| (1) |
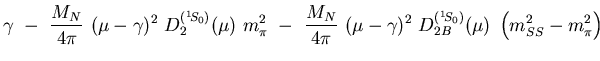 |
|||
![$\displaystyle +\
{g_A^2 M_N\over 8\pi f^2}\left[\
m_\pi^2\log\left({\mu\over m_\pi}\right) +\
(m_\pi-\gamma)^2 - (\mu-\gamma)^2 \right]$](img73.png) |
|||
![$\displaystyle +\
{g_0^2 M_N\over 8\pi f^2}\
\left( m_{SS}^2-m_\pi^2 \righ...
...u\over m_\pi}\right) +\
{1\over 2} - {\gamma \over m_\pi} \right]
,$](img74.png) |
(2) |