An effective field theory with consistent power-counting now exists for nuclear
processes involving momentum
![]() [12],
which allows one to perform systematic calculations of some nuclear observables.
We used it to compute the leading light quark mass,
[12],
which allows one to perform systematic calculations of some nuclear observables.
We used it to compute the leading light quark mass, ![]() , dependence
of observables in the two-nucleon sector,
which is a fundamental aspect of strong interaction physics.
Partial motivation for this work was the experimental hint
that the fundamental constants of nature are time dependent.
If this proves to be the case, the predictions of Big Bang Nucleosynthesis
(BBN) will differ from present calculations which assume time-independent
constants.
In order to address BBN in this scenario
one needs to know how nuclei and nuclear processes depend upon the constants,
including the light-quark masses.
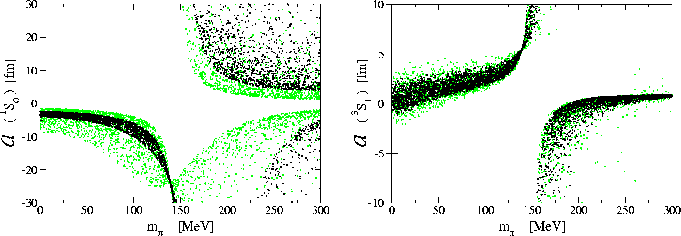
We were able to make rigorous predictions for the quark-mass
dependence of the deuteron binding energy and the scattering length in the
, dependence
of observables in the two-nucleon sector,
which is a fundamental aspect of strong interaction physics.
Partial motivation for this work was the experimental hint
that the fundamental constants of nature are time dependent.
If this proves to be the case, the predictions of Big Bang Nucleosynthesis
(BBN) will differ from present calculations which assume time-independent
constants.
In order to address BBN in this scenario
one needs to know how nuclei and nuclear processes depend upon the constants,
including the light-quark masses.
We were able to make rigorous predictions for the quark-mass
dependence of the deuteron binding energy and the scattering length in the
![]() -channel [13].
It is interesting to note that
BBSvK counting [12] allowed us to derive an analytic expression for the
-channel [13].
It is interesting to note that
BBSvK counting [12] allowed us to derive an analytic expression for the
![]() scattering length as a function of
scattering length as a function of ![]() .
There are uncertainties in the calculations arising from local four-nucleon
.
There are uncertainties in the calculations arising from local four-nucleon
![]() -dependent interactions and from uncertainties in the pion-nucleon interaction in
the single nucleon sector.
It is hoped that the four-nucleon
-dependent interactions and from uncertainties in the pion-nucleon interaction in
the single nucleon sector.
It is hoped that the four-nucleon
![]() -dependent interactions will be determined in lattice simulations at some
point in the future, and that higher precision experiments and calculations
will reduce the uncertainty arising from the single nucleon sector.
-dependent interactions will be determined in lattice simulations at some
point in the future, and that higher precision experiments and calculations
will reduce the uncertainty arising from the single nucleon sector.
 |