

Next: Chiral Symmetry and Isospin
Up: PHYS 560: Lectures During
Previous: Introduction to Nuclear Physics
The underlying theory of strong interactions is Quantum Chromodynamics (QCD),
which is responsible for all strong interaction phenomena.
The QCD lagrange density is
| |
|
![$\displaystyle {\cal L}_{\rm QCD}~=~
\overline{q}_i^a\left[ i{\rm D}\hskip-0.65e...
...p0.2em- m_i\right]_a^b q_b^i
\ -\ {1\over 4} G_{\mu\nu}^A G^{A\ \mu\nu}
\ \ \ ,$](img17.gif) |
(1) |
where 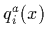 is a quark field operator, where
is a quark field operator, where
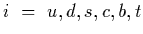 are
the six standard model quarks with mass
are
the six standard model quarks with mass 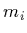 and
and 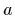 is a colour index that
runs from
is a colour index that
runs from 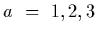 (or red,
green,
blue depending on your taste), e.g.
(or red,
green,
blue depending on your taste), e.g.
| |
|
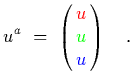 |
(2) |
The covariant derivative that preserves local invariance under
SU(3) color transformations is
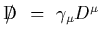 where
where
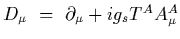 ,
where
,
where 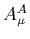 is a gluon field,
is a gluon field,
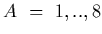 .
The SU(3) field strength tensor is defined through
.
The SU(3) field strength tensor is defined through
![${1\over i g_s}\left[ D_\mu , D_\nu\right]~=~G_{\mu\nu}~=~G_{\mu\nu}^A T^A$](img28.gif) ,
where
,
where 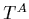 are the SU(3) Gell-Mann matrices, and
are the SU(3) Gell-Mann matrices, and 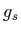 is the strong
interaction coupling ``constant''.
is the strong
interaction coupling ``constant''.
This looks like a very simple theory, there are quarks 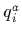 which interact with each other via gluons
which interact with each other via gluons 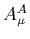 .
This part looks exactly like electromagnetism, however there is a beast hidden
in
.
This part looks exactly like electromagnetism, however there is a beast hidden
in
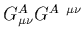 ,
and that is the non-linear interaction between
gluons. Unlike photons which do not interact with themselves (Maxwells
equations are linear), the eight gluons can interact with each other through
the three and four gluon interactions, a generic feature of a non-abelian
theory (Yang-Mills theory).
Through quantum fluctuations these interactions make the strong coupling
,
and that is the non-linear interaction between
gluons. Unlike photons which do not interact with themselves (Maxwells
equations are linear), the eight gluons can interact with each other through
the three and four gluon interactions, a generic feature of a non-abelian
theory (Yang-Mills theory).
Through quantum fluctuations these interactions make the strong coupling
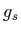 depend upon the scale at which the particular process is occurring,
i.e. it is not constant.
Even more interesting is that
depend upon the scale at which the particular process is occurring,
i.e. it is not constant.
Even more interesting is that 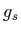 gets larger for smaller momentum transfers
(long-distances) and weaker for high momentum transfers (short-distances).
This is called asymptotic freedom.
Numerous experiments have been performed over the last few years and
theoretical techniques developed to determine the value of
gets larger for smaller momentum transfers
(long-distances) and weaker for high momentum transfers (short-distances).
This is called asymptotic freedom.
Numerous experiments have been performed over the last few years and
theoretical techniques developed to determine the value of 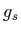 in the region
where it is small.
I have ``borrowed'' (without permission from the ALEPH Collaboration
website[2]) a plot of the coupling as a function
of the ``scale'' at which the process is occurring.
In fig. (1) the quantity
in the region
where it is small.
I have ``borrowed'' (without permission from the ALEPH Collaboration
website[2]) a plot of the coupling as a function
of the ``scale'' at which the process is occurring.
In fig. (1) the quantity
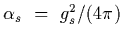 is plotted.
is plotted.
Figure:
The strong interaction coupling constant
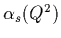 as a function of
as a function of 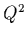 .
.
![\includegraphics[width=5in]{/home/savage/Teaching/Class560/Lec560_1/alphas.ps}](img34.gif)
|
Eventually, as the momentum-scale becomes smaller, i.e. we look at processes
involving larger and larger distance scales, the coupling constant becomes
large, too large for a perturbative treatment.
The theory becomes non-perturbative and in this regime the quarks and gluons
are no-longer perturbatively close to what the ``in'' and ``out'' states of
a particular interaction process look like.
In fact, no-one has ever observed an isolated quark or gluon....there is no
evidence that free quarks or gluons exist. In fact the interaction between
them become so strong that they ALWAYS bind into hadrons, such as protons,
neutrons, pions,  's and so forth.
These are states that are singlet under SU(3) colour transformations
(it is worth spending a few minutes looking at the particle data book to see
what we know about the observable hadrons).
Thus, if we are interested in the low-momentum interactions of, say,
nucleons then it is clear that we cannot use a perturbative approach in terms
of quark and gluon fields and we have to develop a theory that is written
entirely in terms of hadronic fields.
A somewhat more technical description goes along the lines of the
approximate
's and so forth.
These are states that are singlet under SU(3) colour transformations
(it is worth spending a few minutes looking at the particle data book to see
what we know about the observable hadrons).
Thus, if we are interested in the low-momentum interactions of, say,
nucleons then it is clear that we cannot use a perturbative approach in terms
of quark and gluon fields and we have to develop a theory that is written
entirely in terms of hadronic fields.
A somewhat more technical description goes along the lines of the
approximate
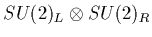 chiral symmetry of the lagrange density in
eq. (1) is spontaneously broken to
chiral symmetry of the lagrange density in
eq. (1) is spontaneously broken to 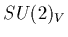 ,
by an non-zerop
value of
,
by an non-zerop
value of
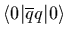 .
What all of this means will be covered in the next quarter.
During this quarter we will study the phenomenology of the hadronic theory and
look for ``exact'' results basd on the symmetries of QCD where they exist.
.
What all of this means will be covered in the next quarter.
During this quarter we will study the phenomenology of the hadronic theory and
look for ``exact'' results basd on the symmetries of QCD where they exist.
A feature that is obvious but one that we have not stressed is that the
strong interactions between quarks and gluons doe NOT depend upon the
flavor of the quark.
The coupling between gluons and the 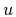 -quark is the same as the coupling
between gluons and the
-quark is the same as the coupling
between gluons and the 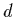 -quark.
The two differences between the quarks are firstly their masses, and secondly
their electric charges.
-quark.
The two differences between the quarks are firstly their masses, and secondly
their electric charges.


Next: Chiral Symmetry and Isospin
Up: PHYS 560: Lectures During
Previous: Introduction to Nuclear Physics
Martin Savage
1999-10-04
![$\displaystyle {\cal L}_{\rm QCD}~=~
\overline{q}_i^a\left[ i{\rm D}\hskip-0.65e...
...p0.2em- m_i\right]_a^b q_b^i
\ -\ {1\over 4} G_{\mu\nu}^A G^{A\ \mu\nu}
\ \ \ ,$](img17.gif)
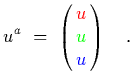
![]() which interact with each other via gluons
which interact with each other via gluons ![]() .
This part looks exactly like electromagnetism, however there is a beast hidden
in
.
This part looks exactly like electromagnetism, however there is a beast hidden
in
![]() ,
and that is the non-linear interaction between
gluons. Unlike photons which do not interact with themselves (Maxwells
equations are linear), the eight gluons can interact with each other through
the three and four gluon interactions, a generic feature of a non-abelian
theory (Yang-Mills theory).
Through quantum fluctuations these interactions make the strong coupling
,
and that is the non-linear interaction between
gluons. Unlike photons which do not interact with themselves (Maxwells
equations are linear), the eight gluons can interact with each other through
the three and four gluon interactions, a generic feature of a non-abelian
theory (Yang-Mills theory).
Through quantum fluctuations these interactions make the strong coupling
![]() depend upon the scale at which the particular process is occurring,
i.e. it is not constant.
Even more interesting is that
depend upon the scale at which the particular process is occurring,
i.e. it is not constant.
Even more interesting is that ![]() gets larger for smaller momentum transfers
(long-distances) and weaker for high momentum transfers (short-distances).
This is called asymptotic freedom.
Numerous experiments have been performed over the last few years and
theoretical techniques developed to determine the value of
gets larger for smaller momentum transfers
(long-distances) and weaker for high momentum transfers (short-distances).
This is called asymptotic freedom.
Numerous experiments have been performed over the last few years and
theoretical techniques developed to determine the value of ![]() in the region
where it is small.
I have ``borrowed'' (without permission from the ALEPH Collaboration
website[2]) a plot of the coupling as a function
of the ``scale'' at which the process is occurring.
In fig. (1) the quantity
in the region
where it is small.
I have ``borrowed'' (without permission from the ALEPH Collaboration
website[2]) a plot of the coupling as a function
of the ``scale'' at which the process is occurring.
In fig. (1) the quantity
![]() is plotted.
is plotted.
![]() -quark is the same as the coupling
between gluons and the
-quark is the same as the coupling
between gluons and the ![]() -quark.
The two differences between the quarks are firstly their masses, and secondly
their electric charges.
-quark.
The two differences between the quarks are firstly their masses, and secondly
their electric charges.