As we know the nucleon is not a fundamental object,
it will come as no surprise
to learn that it has excited states.
One lowest lying excitation that couples incredibly strongly to ![]() is the
is the ![]() ,
which is shorthand for
,
which is shorthand for
![]() ,
,
![]() ,
,
![]() and
and
![]() ,
an isospin quartet of particles.
They have masses
,
an isospin quartet of particles.
They have masses
![]() and widths
and widths
![]() .
When we neglect electromagnetic and weak interactions these hadrons are almost
identical, and can be assigned to an irreducible representation of SU(2).
.
When we neglect electromagnetic and weak interactions these hadrons are almost
identical, and can be assigned to an irreducible representation of SU(2).
To figure out how the ![]() 's are assigned to the totally symmetric tensor
's are assigned to the totally symmetric tensor
![]() ,
with
,
with
![]() (it is easy to show that this has four independent entries,
further if it had a
component that was antisymmetry under interchange of two indices,
then it could
be contracted with
(it is easy to show that this has four independent entries,
further if it had a
component that was antisymmetry under interchange of two indices,
then it could
be contracted with
![]() ),
we look at the free hamiltonian for non-relativistic particles, which for
nucleons is
),
we look at the free hamiltonian for non-relativistic particles, which for
nucleons is
![$\displaystyle {\cal H}_{\rm free}~=~N^{a, \dagger} \left[ -{\nabla^2\over 2 M_N}\right]
N_a
\ \ \ ,$](img167.gif) |
(27) |
The relation between strong decay rates
![]() can be found
be the two methods we have used previously.
Let us determine the ratio of decay rates for
can be found
be the two methods we have used previously.
Let us determine the ratio of decay rates for
![]() and
and
![]() .
Firstly, using states
.
Firstly, using states
![$\displaystyle \langle p\pi^+\vert\Delta^{++}\rangle~=~
\left[\langle {1\over 2},{1\over 2}\vert\langle 1,1\vert\right]\vert{3\over 2}, {3\over
2}\rangle$](img177.gif) |
|||
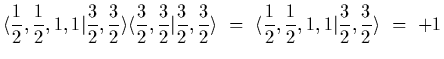 |
|||
![$\displaystyle \langle n\pi^+\vert\Delta^{+}\rangle~=~
\left[\langle {1\over 2},-{1\over 2}\vert\langle 1,1\vert\right]\vert{3\over 2}, {1\over
2}\rangle$](img179.gif) |
|||
![$\displaystyle \ =\ \left[
\langle {1\over 2},-{1\over 2},1,1\vert{3\over 2},{1\...
...langle {1\over 2}, {1\over 2}\vert
\right]
\ \vert{3\over 2}, {1\over 2}\rangle$](img180.gif) |
|||
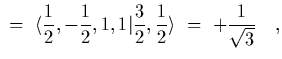 |
(31) |
Solving the same problem using tensors we have and effective hamiltonian of the
form
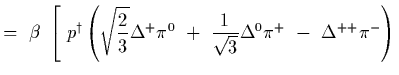 |
|||
![$\displaystyle \left.\ +\
n^\dagger \left( \sqrt{2\over 3}\Delta^0\pi^0
\ +\ {1\...
...sqrt{3}}\Delta^-\pi^+
\ -\ {1\over\sqrt{3}}\Delta^+\pi^-
\right)\
\right]
\ \ ,$](img185.gif) |
(32) |
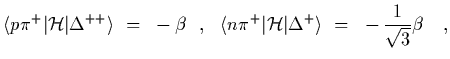 |
(33) |