Let us begin by considering the interaction strengths between nucleons and
pions.
We would like to know, on the basis of isospin symmetry alone (neglecting
isospin breaking) the relative size of the interaction between, say,
![]() and
and ![]() ,
when all other quantum numbers are the same.
,
when all other quantum numbers are the same.
Using states we would go about this by asking about the overlap of states
of isospin, we start by combining the ![]() states into states to total
isospin,
states into states to total
isospin,
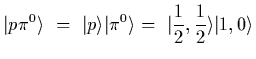 |
|||
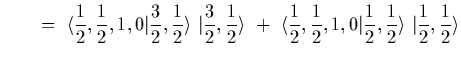 |
|||
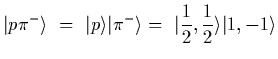 |
|||
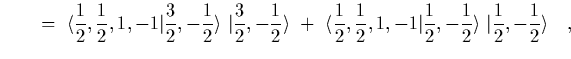 |
(23) |
We can arrive at the same result by considering the tensors describing the
![]() and
and ![]() fields.
In the limit we are considering the world is invariant under
arbitrary isospin rotations, and therefore, the hamiltonian describing the
world is a singlet in iso-space, i.e. no spare isospin indices are left
floating around.
The most general form for the
effective interaction hamiltonian between nucleons and one
pion is, considering only isospin structure and using eqs. (21)
and (12),
fields.
In the limit we are considering the world is invariant under
arbitrary isospin rotations, and therefore, the hamiltonian describing the
world is a singlet in iso-space, i.e. no spare isospin indices are left
floating around.
The most general form for the
effective interaction hamiltonian between nucleons and one
pion is, considering only isospin structure and using eqs. (21)
and (12),
![$\displaystyle =~ \alpha\ \left[
{1\over\sqrt{2}} p^\dagger p\pi^0\ +\
p^\dagger...
...i^+\ +\
n^\dagger p\pi^0\ -\
{1\over\sqrt{2}} n^\dagger n\pi^0\ \right]
\ \ \ ,$](img155.gif) |
(25) |
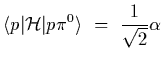 |
|||
| (26) |
The method of tensors is much more versatile than using tabulated CG's, as it easily extends to other group structures like SU(3) etc. It is also clearly connected to the Wigner-Eckart theorem.