Chapter 43: Problem 14

Question: A bottom-weighted $2~{\rm m}$ long vertical pole extends from the bottom of a swimming pool to a point $d~=~0.64~{\rm m}$ above the water. Sunlight is incident at $\phi_1~=~55^o$ above the horizon. Find the length of the shadow of the pole on the level bottom of the pool.

Solution: We follow the light that just passes over the top of the pole standing up out of the pool. It travels a horizontal distance d₁ before hitting the top of the water and then an additional horizontal distance d₂ after entering the water. We are interested in the sum d₁+d₂, the length of the shadow in the pool. By considering triangles,

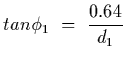$$tan\phi_1~=~{0.64\over d_1}$$

which gives $d_1~=~0.448~{\rm m}$. Upon entering the pole, the angle wrt the normal is found from $n_1\sin\theta_1~=~n_2\sin\theta_2$. Using, $\theta_1~=~90-\phi_1~=~35^o$, n₁ = 1 and n₂ = 1.33, we find $\theta_2~=~25.55^o$. The length $d_2~=~1.36\tan\theta_2~=~0.65~{\rm m}$. Therefore we have a shadow of length $d_1+d_2~=~1.098~{\rm m}$.