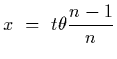 |
where n is the refractive index and
Question: Prove that a ray incident oin the surface of a sheet of plate glass of thickness t emerges from the opposite face parallel to its incident direction but displaced sideways, as in Fig 30, Chap 43.
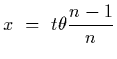 |
Solution: For small angles we have that
![]() becomes
becomes
![]() .
For small angles, the displacement of the ray in the absence of the glass is
.
For small angles, the displacement of the ray in the absence of the glass is
![]() ,
and the for the ray in the glass is
,
and the for the ray in the glass is
![]() ,
and
therefore, we find the difference to be
,
and
therefore, we find the difference to be
![]() ,
which reproduces the required result when n1 = 1 and n2 = n.
For part (b), one simply puts in the values of n = 1.55,
,
which reproduces the required result when n1 = 1 and n2 = n.
For part (b), one simply puts in the values of n = 1.55,
![]() ,
and
,
and
![]() to find
to find
![]() .
.