Positivity and analytic properties of QCD Green functions

R. Alkofer (Tubingen University), W. Detmold, C.S. Fisher and P. Maris (NCSU)

The Euclidean structure of the quark, gluon and ghost propagators from lattice QCD and DSE studies is examined from the point of view of positivity and confinement [38]. For a Euclidean momentum-space propagator, $D(p)$, the behavior of the function

$$\Delta(T)=\int d^3x \int \frac{d^4p}{(2\pi)^4} e^{i p\cdot x} D(p)$$

has implications for the appearance of the corresponding particle in the physical theory. Violation of Osterwalder-Schrader reflection positivity ( $\sim\Delta(T)<0$) for a given propagator guarantees that the corresponding particle is not in the (semi-positive definite) physical state space of the theory. Such positivity violations are thus a sufficient (but not necessary) condition for confinement.

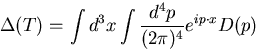
Both lattice and recent DSE studies show evidence for positivity violation in the gluon propagator (and trivially in the (negative metric) ghost propagator). The situation for the quark propagator is less clear; the analytic structure of the quark propagator and the (non)positivity of solutions of the quark DSE appears to be sensitive to the presence of a scalar contribution in the quark gluon vertex (expected from gauge symmetry). Studying the behavior of the function $\Delta(T)$ allows possible complex plane parameterizations of propagators to be investigated. Such parameterizations can also be constrained from existing lattice data.