

Next: Bibliography
Up: PHYS 560: Lectures During
Previous: Quadrupole Interactions.
The quadrupole moment of the deuteron is
 .
Writing the wavefunction of the deuteron as we have before as
.
Writing the wavefunction of the deuteron as we have before as
| |
|
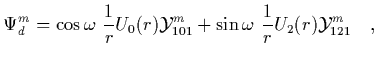 |
(49) |
we have that
| |
|
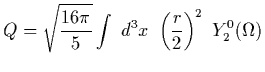 |
|
| |
|
![$\displaystyle = \sqrt{ \pi\over 5}
\int\ dr\ r^2\ d\Omega\ r^2 Y_2^0(\Omega)\ {...
...ga\cos\omega {\cal Y}^{1*}_{121}{\cal Y}^1_{101} U_0 (r) U_2(r)
\right]
\ \ \ .$](img209.gif) |
(50) |
You will recall that
| |
|
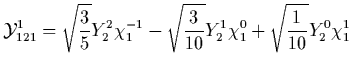 |
|
| |
|
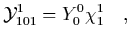 |
(51) |
which leads to
| |
|
![$\displaystyle Q = {1\over 5\sqrt{2}} \int\ dr r^2
\left[\sin\omega\cos\omega\ U_0(r) U_2(r)
- {1\over\sqrt{2}} \vert U_2(r)\vert^2 \sin^2\omega
\right]
\ \ \ .$](img212.gif) |
(52) |
We notice that a pure D-state has a  quadrupole moment.
It is clear that we must have a non-trivial
amount of S-D mixing in order to obtain a
quadrupole moment.
It is clear that we must have a non-trivial
amount of S-D mixing in order to obtain a  quadrupole
moment as is observed for the deuteron.
We recall that the deuteron magnetic moment indicated
quadrupole
moment as is observed for the deuteron.
We recall that the deuteron magnetic moment indicated
 .
Inserting this value into eq. (52) and using the measured
value of
.
Inserting this value into eq. (52) and using the measured
value of  we find that
we find that
 ,
entirely consistent
with the size of the deuteron we have
determined from scattering.
,
entirely consistent
with the size of the deuteron we have
determined from scattering.
We should also note at this stage that it might appear that
the quadrupole moment is a better observable
from which to extract
 .
The magnetic moment
contribution from the D state is small and hence
yields a large uncertainty compared to
.
The magnetic moment
contribution from the D state is small and hence
yields a large uncertainty compared to  .
However, you will also recall that the magnetic moment was
independent of the radial wavefunctions and hence the
nucleon-nucleon potential. This is not true of the
quadrupole moment that depends directly on both the
S and D wave radial wavefunctions.
.
However, you will also recall that the magnetic moment was
independent of the radial wavefunctions and hence the
nucleon-nucleon potential. This is not true of the
quadrupole moment that depends directly on both the
S and D wave radial wavefunctions.


Next: Bibliography
Up: PHYS 560: Lectures During
Previous: Quadrupole Interactions.
Martin Savage
1999-10-19
![]() .
Writing the wavefunction of the deuteron as we have before as
.
Writing the wavefunction of the deuteron as we have before as
![]() .
The magnetic moment
contribution from the D state is small and hence
yields a large uncertainty compared to
.
The magnetic moment
contribution from the D state is small and hence
yields a large uncertainty compared to ![]() .
However, you will also recall that the magnetic moment was
independent of the radial wavefunctions and hence the
nucleon-nucleon potential. This is not true of the
quadrupole moment that depends directly on both the
S and D wave radial wavefunctions.
.
However, you will also recall that the magnetic moment was
independent of the radial wavefunctions and hence the
nucleon-nucleon potential. This is not true of the
quadrupole moment that depends directly on both the
S and D wave radial wavefunctions.