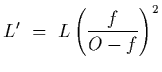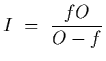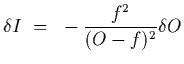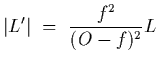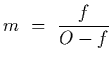

Next: Chapter 44: Problem 7
Up: Waves and Optics, Solutions
Previous: Chapter 44: Problem 4
Question: A short linear object of length L lies on the axis of a
spherical mirror, a distance O from the mirror.
Show that its image will have length 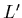
Show that the longitudinal magnification
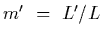 is equal to m2 where m is the lateral magnification.
is equal to m2 where m is the lateral magnification.
Solution:
From previous problem,
and by taking small variations, we have that
and hence
Now we know that m = -I/O, which is
from which it is clear that
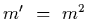 .
.


Next: Chapter 44: Problem 7
Up: Waves and Optics, Solutions
Previous: Chapter 44: Problem 4
Martin Savage
1999-02-10
![]()