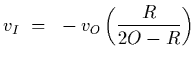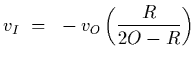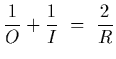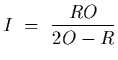

Next: Chapter 44: Problem 5
Up: Waves and Optics, Solutions
Previous: Chapter 44: Problem 1
Question: A Luminous point is moving at speed vO toward a spherical
mirror, along its axis.
Show that the speed of its image is moving at
Assume that the mirror is concave, with
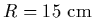 and
and
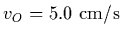 .
Find the speed of the image if the object is far outside the focal point
(
.
Find the speed of the image if the object is far outside the focal point
(
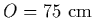 ), if it is near the focal point (
), if it is near the focal point (
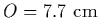 )
and close to the mirror (
)
and close to the mirror (
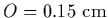 ).
).
Solution: For an oject located at O, we know that the image is located
at
which can be written as
Taking a single time derivative gives
which is what we are required to prove.
- 1.
-
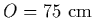 gives
gives
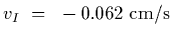
- 2.
-
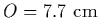 gives
gives
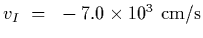
- 3.
-
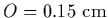 gives
gives
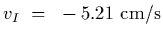


Next: Chapter 44: Problem 5
Up: Waves and Optics, Solutions
Previous: Chapter 44: Problem 1
Martin Savage
1999-02-10