Chapter 43: Problem 8

Question: Ocean waves moving at a speed of $v_1~=~4.0~{\rm m/s}$ are approaching a beach at an angle of $\theta_1~=~30^o$ to the normal, as shown in Fig27 Chap 43. Suppose the water depth changes abruptly and the wave speed drops to $v_2~=~3.0~{\rm m/s}$. Close to the beach, what is the angle $\theta_2$ between the direction of the wave motion and the normal? Use Snells Law (and more appropriately Fermats Principle). Explain why waves come in normal to the shore even though at large distances they approach at a variety of angles.

Solution: We have that

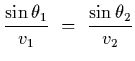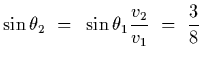$${\sin\theta_1\over v_1}~=~{\sin\theta_2\over v_2}$$

From which we see that

$$\sin\theta_2~=~\sin\theta_1 {v_2\over v_1}~=~{3\over 8}$$

giving $\theta_2~=~22^o$. As waves approach the shore their speed is reduced significantly, and therefore, the angle must also be reduced significantly, according to the refraction laws.