Chapter 20: Problem 30

Question:        A sound wave of $\lambda=0.42\ {\rm m}$ wavelength enters the tube shown in Fig. 19 (chap.20). What must be the smallest radius r such that a minimum will be heard at the detector?

Solution:         We require that the path difference between traveling along the straight path and traveling along the semi-circular path is equal to ${\lambda\over 2}$.

$$\pi r - 2 r {\lambda\over 2}$$ =

$${\lambda\over 2(\pi-2)} = 0.184\ {\rm m} \ \ \ .$$ r = 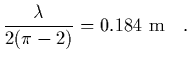(6)