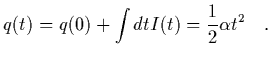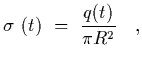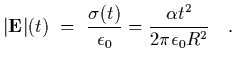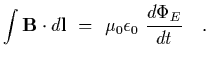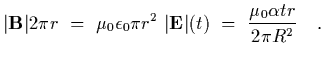

Next: About this document ...
Up: Waves and Optics, Solutions
Previous: Chapter 40: Problem 11
Question:
A long cylindrical conducting rod with radius R is
centered on the x- axis as shown in Fig. 12 (chap 40).
A narrow saw cut is made in the rod at x=b.
A conduction current i increasing with time and
given by
 flows toward the right of
the rod,
flows toward the right of
the rod,  is a positive constant of proportionality.
At t=0 there is no charge on the cut faces near x=b.
is a positive constant of proportionality.
At t=0 there is no charge on the cut faces near x=b.
- 1.
- Find the magnitude of the charge on these
faces as a function of time.
- 2.
- Use Eq.I in table 2 to find E in the
gap as a function of time.
- 3.
- Sketch the field lines of B for
r<R where r is the distance
from the x- axis.
- 4.
- Use Eqn IV in Table 2 to find B(r) in the gap for r<R
- 5.
- Compare the above answer with B(r) in the rod for r<R
Solution:
If q (t) is the charge on each face of the gap
as a function of time, then
| |
|
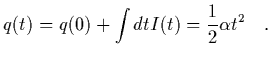 |
(20) |
The charge density on the plates is thus
| |
|
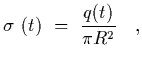 |
(21) |
giving an electric field in the gap of
| |
|
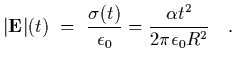 |
(22) |
From this we can use Amperes law to find the magnetic field,
| |
|
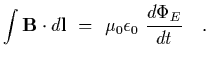 |
(23) |
| |
|
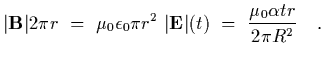 |
(24) |
Now, to compute B inside the rod, we assume a uniform current density, and
use
This is the same expression.


Next: About this document ...
Up: Waves and Optics, Solutions
Previous: Chapter 40: Problem 11
Martin Savage
1999-01-21
![]() flows toward the right of
the rod,
flows toward the right of
the rod, ![]() is a positive constant of proportionality.
At t=0 there is no charge on the cut faces near x=b.
is a positive constant of proportionality.
At t=0 there is no charge on the cut faces near x=b.