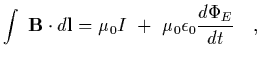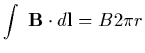
Chapter 40: Problem 11

Question: A parallel plate capacitor with circular plates in diameter $2~R~=~0.216~{\rm m}$ is being charged as in Fig. 2 (chap 40). The displacement current density throughout the region is uniform, into the paper in the diagram, and has a value of $j_d~=~1.87~{\rm mA/cm^2}$.

1.

Calculate the magnetic field B at a distance $r~=~53.0~{\rm mm}$ from the axis of symmetry of the region.

2.

Calculate the time derivative of the electric field in this region.

Solution:         We use Amperes law including the displacement current

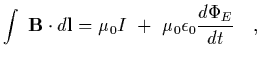$$\int\ {\bf B}\cdot d{\bf l} =\mu_0 I \ +\ \mu_0\epsilon_0 {d\Phi_E\over dt} \ \ \ ,$$ (17)

and for the system of interest (the surface contained inside the gap between the plates) I=0. The integral is around a closed loop. Given the cylindrical symmetry of the problem, we have that

$$\int\ {\bf B}\cdot d{\bf l} = B 2\pi r$$

$$\mu_0\epsilon_0 {d\Phi_E\over dt} = \mu_0 \int d{\bf A}\cdot {\bf j_d}\ = \pi r^2 \vert{\bf j_d}\vert$$

$$\vert{\bf B}\vert = {1\over 2} \mu_0 \vert{\bf j_d}\vert r\ =\ 6.23\times 10^{-7}\ T \ \ \ .$$ (18)

To get the time derivative of the electric field, see that

$$I_d = \epsilon_0 {d\Phi_E\over dt}$$

$$\vert{\bf j_d}\vert\ \pi r^2 = \pi r^2 \epsilon_0{d \vert{\bf E}\vert\over dt}$$

$${d \vert{\bf E}\vert\over dt} = { \vert{\bf j_d}\vert\over \epsilon_0} \ =\ 2.11\times 10^{12}\ {\rm V/(m.s)} \ \ \ .$$ (19)