for spin-
fields
fieldsIan D. Lawrie
Department of Physics and Astronomy, University of Leeds
In this talk, I describe a partial resummation of perturbation theory that I think is useful
when one wishes to follow the evolution in time of a system that is not close to equilibrium.
In the simplest case of a scalar field theory, ordinary perturbation theory uses bare
time-ordered propagators of the form
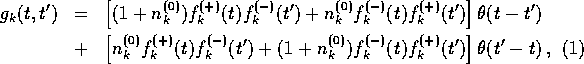
together with anti-time-ordered and Wightman functions of a similar kind. In this expression
(which applies to a spatially homogeneous system), the mode functions 
for
particle modes of momentum k are solutions
of the equation
where the differential operator 
is that associated with the quadratic part of the
action 
. The numbers 
are the
occupation numbers of these modes that characterize an initial state set up, say, at t=0. These
occupation numbers are problematic in the following sense. If there are interactions that cause
scattering, one would expect the state of the system at time t to be characterized by
quasiparticle excitations of finite width, say 
, whose occupation numbers 
evolve with a relaxation time of the order of 
. Thus, propagators of the form (1)
provide a useful description only for times 
.
The purpose of the resummation I will describe, then, is to obtain a modified perturbative scheme in which
the lowest-order propagators take at least approximate account of the evolution of the non-equilibrium state, so
as to be useful over extended periods of time. Broadly, the aim is to describe this state in terms of its own
quasiparticle excitations rather than single-particle excitations of the vacuum. This means finding an optimal
means of splitting the action I into an unperturbed part 
that (loosely speaking) describes free quasiparticles,
and an interaction 
that accounts for their interactions. Since only Gaussian path integrals can be
computed exactly, should be quadratic in the fields. I will therefore write
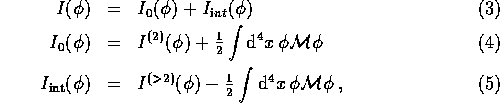
where is the part of the original action I that is quadratic in the fields and 
is the rest of it.
A partial resummation of the perturbation series for the full 2-point functions is effected by asking the
counterterm 
that appears in to cancel some part of the loop contributions to the
self energy. The central issue to be addressed is how to construct a suitable differential operator
or, equivalently, a lowest-order action and the propagators associated with it. I will first review how
this can be done for a scalar field [1] and then describe the extent to which I have been able to
do something similar for a spin- field.
Here, I consider explicitly the usual 
theory, defined by the Lagrangian density
but the strategy I describe should apply equally well when the scalar field 
is embedded in some
larger theory. I consider only a spatially homogeneous system, but allow for a time-dependent mass m(t)
which drives this system away from equilibrium. For example, the theory of a scalar field in a Robertson-Walker
universe can be cast in the form of a Minkowski-space theory with time-dependent mass. To be concrete,
suppose that an initial state of thermal equilibrium with inverse temperature 
is set up at time t=0.
Then the standard closed-time-path formalism yields a path integral weighted by the action
where the path-integration variables 
, 
and 
live on a closed contour in the complex time
plane. The Euclidean action 
(which uses m(0)) represents the initial density matrix. In this
theory, there is a 
matrix of 2-point functions 
, with a, b = 1, 2, 3, but I will need to
think explicitly only about the real-time functions, with a, b = 1, 2. For the real-time part of the action, I want to
construct a lowest-order version 
, where, after a
spatial Fourier transform, the differential operator 
is
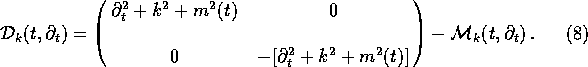
Subject to several constraints (about which I will be more explicit when I discuss spinor fields in detail),
the most general choice for is
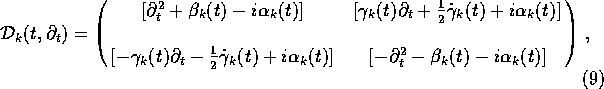
where 
, 
and are real functions yet to be determined. Of course, the
counterterm can be read off from (8) and (9).
The 
matrix of propagators 
is the solution (subject to suitable boundary conditions)
of
Suppressing the spatial momentum k, which is omnipresent, this solution can be written in terms of a single
complex function h(t,t') as
where 
and 
. The function h is
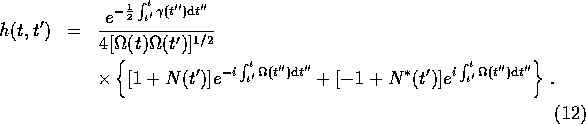
We see that one of the undetermined functions, , can be interpreted as a quasiparticle
width. The quasiparticle energy 
is a solution of
Finally, the function 
, which I hope to interpret in terms of time-dependent occupation numbers, is a
solution of
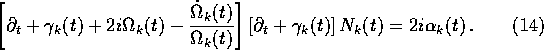
To give substance to the scheme I have described so far, a prescription is needed for determining the three
functions , and introduced in (9). To this end, define the
self energy matrix 
by
This self energy has contributions from the counterterm and from loop diagrams:
The general strategy is to optimize as an approximation to the full two-point functions 
by
arranging for to cancel some part of 
. Clearly, since is non-local
in time, only a partial cancellation can be achieved. Various prescriptions might be possible; perhaps the most
obvious is the following. Express in terms of the average time 
and the difference
(t-t') and Fourier transform on (t-t'). The components of 
contain at most one time
derivative, so the self energy can be decomposed into contributions that are even and odd in the frequency:
Generalized gap equations to be solved for , and can now be obtained
by requiring
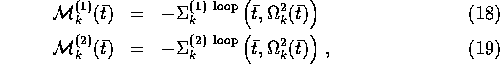
which amounts to an on-shell renormalization prescription.
These gap equations provide exact implicit definitions of , and , but they
cannot, of course, be exactly solved. If the perturbative expansions for 
and
are truncated at some finite order, one obtains concrete expressions for them
in terms of the propagators . These truncated gap equations, together with equation (13)
for the quasiparticle energy and (14) for the function form a closed system that one might try
to solve numerically. It is to some extent illuminating to establish a connection with kinetic theory through
some further approximations.Suppose that the gap equations are truncated at two-loop order - the lowest
order that yields a nonzero quasiparticle width . Then, assuming sufficiently weak coupling
and sufficiently slow time evolution, propagators inside the loop diagrams can be approximated by
taking 
and the limit 
. Then,
with quasiparticle occupation numbers defined by
a time-derivative expansion of (14), yields the Boltzmann-like equation
fields
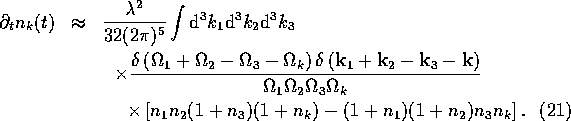
I will now describe an attempt to apply a similar analysis to the case of spinor fields. This is
somewhat more complicated. For reasons that will become apparent, I have achieved so far only
a restricted version of the solution and even this has features for which I have no clear interpretation.
For purposes of illustration, I will have in mind a simple theory of the form
but again the strategy should apply to more general theories containing spinors. If the
particles are heavy enough to decay into two 
particles, then the one-loop self energy for
has an imaginary part which gives the a finite thermal width. As before, I plan to
construct a lowest-order action 
such that the propagator matrix S, which is a solution of
incorporates this thermal width and evolving quasiparticle occupation numbers. I continue to deal
with a spatially homogeneous system and will henceforth suppress all momentum arguments. The
first step towards constructing a suitable differential operator is to obtain some general
properties of the full two-point functions 
and to insist that these be shared by the
lowest-order propagators S(t,t'). The form of is then constrained by the requirement that
(23) admit a solution having these properties.
The full two-point functions are
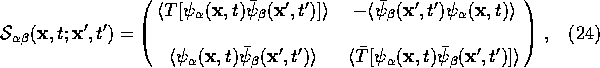
where 
and are spinor indices. The Wightman function
can be written as
To simplify matters, I will assume that the chemical potential for particles is zero. Then,
using the hermiticty of the density operator, it is simple to show that
where, for any Dirac matrix 
, I define 
.
It would be helpful if, as in the scalar theory, the second Wightman function
could be expressed in terms of the
same matrix 
. To this end, I will construct so as to be CP invariant.
This does not imply that the whole theory need be CP invariant - only that CP-violating parts of the
full two-point functions will not be resummed. For the purpose of establishing the structure of ,
however, I suppose that the full two-point functions 
do belong to a CP-invariant theory. In that
case, it turns out that
The CP conjugate of a Dirac matrix is
, where C is the charge conjugation
matrix and 
denotes the transpose.
After a spatial Fourier transform, the full CP-invariant two-point
functions are now given by
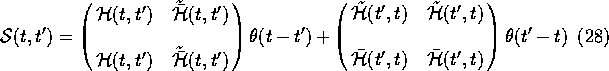
and I will require the unperturbed propagators S(t,t') associated with to have the same structure:
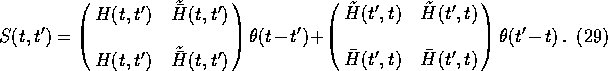
The fact that the Wightman functions have unique values at t=t' implies that
and the canonical anticommutation relation 
implies that
I now look for a differential operator 
such that the equation (23) will admit a
solution of the form (29). The 
arises from the derivative of 
and, if I insist only
on the boundary conditions (30) and (31), then 
and 
can
have only a single time derivative, with coefficient 
, while 
and 
can have no time derivatives at all. (In the scalar case, similar considerations restrict the diagonal elements
of to have at most two time derivatives and the off diagonal elements to have at most one. In principle,
one might allow arbitrary numbers of time derivatives, with enough boundary conditions to eliminate the
consequent derivatives of , but I have not found such a scheme tractable.) Finally, causality
requires that
With these restrictions, the most general form of is
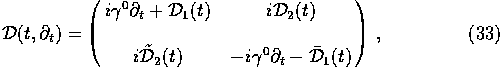
where the as yet undetermined matrices 
and 
satisfy
The general procedure would now be to expand the 
in a complete basis of Dirac matrices
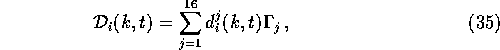
the functions 
being the analogues of , and that
appeared in the scalar theory. However, I have not yet found the energy to solve this general problem.
I will therefore consider a restricted version using a minimal subset of the full Dirac basis, closed under
multiplication, that contains the matrices 1, 
and 
appearing in the free
theory. (``1'' of course denotes the unit matrix.) A convenient basis is
Taking account of the restrictions (34), I get
There are thus 7 as yet undetermined real functions of t and momentum k (which I here reinstate for emphasis),
namely 
, 
, 
and the real and imaginary parts of 
and 
.
With given by (33) and S(t,t') by (29), the equation (23) for the
propagators reduces to the pair
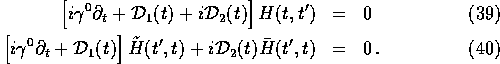
Because the basis (36) is closed under multiplication, (and because the coefficient of in
(39) is 
) the solution for H(t,t') can be written as
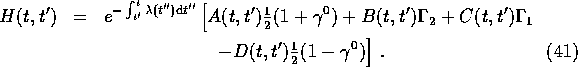
Evidently, the function can be identified as a thermal quasiparticle width. The homogeneous
equation (39), involving the first time argument of H(t,t') becomes
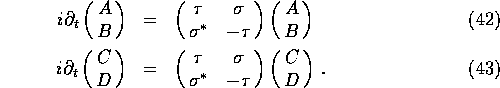
For orientation, I remark that, if were taken as simply the quadratic part of (22), we
would have 
and 
. The hermitian matrix
has real eigenvalues 
, where
is the quasiparticle energy. If 
are the corresponding eigenvectors, then the two solutions
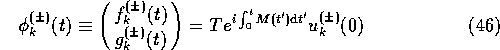
are positive- and negative-energy solutions at the initial time t=0. These two solutions are orthogonal
under the inner product 
(which is preserved by the time evolution) and
are related by
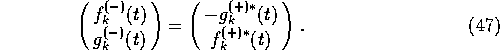
When and are slowly varying, a useful adiabatic approximation is
Evidently, the solution of (39) is
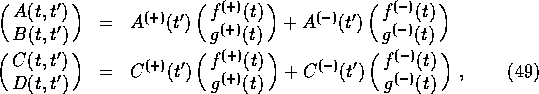
where the coefficients 
and 
are to be found by solving (40) and applying
suitable boundary conditions.
To solve (40), form the linear combinations
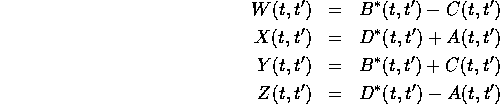
Then(40) becomes
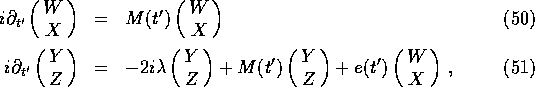
where 
is the matrix
The solution of (50) is, of course
The solution of (51) is not of this form, but since 
and 
are linearly independent
vectors, it can be written as
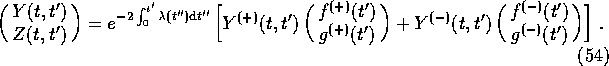
The residual t' dependence of 
will shortly find an interpretation in terms of time-dependent
quasiparticle occupation numbers. These functions are solutions of
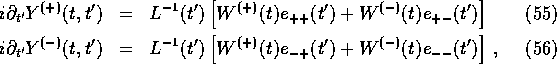
with 
, and
These equations can, of course, be formally integrated, but in the form given they will become kinetic equations.
The solutions (53) and (54) represent, of course, the same functions as
(49). By comparing these two representations, we can determine the coefficients ,
and 
up to constants, which are themselves determined by boundary conditions.
In this way, the propagators (29) are given through the matrix H(t,t') (equation (41) in terms of the function
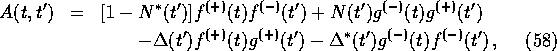
together with B(t,t'), C(t,t') and D(t,t'), for which similar expressions can be written down. The function
N(t'), which multiplies products of one positive-frequency mode and one negative-frequency mode, can
clearly be indentified as a quasiparticle occupation number. It is a solution of
which, with a reasonable prescription for determining 
, etc. will become a Boltzmann equation.
The function 
is a solution of
This looks like a second kinetic equation. However, appears as the coefficient of products
of two positive-frequency or two negative-frequency mode functions, which have no counterpart in the
free-particle propagator, and I have been able to find no simple interpretation for it. In the case of a system
that starts at t=0 from a state of thermal equilibrium, continuity conditions on the complete time path
yield initial conditions for (59) and (60), which are
Finally, a prescription for determining the seven functions , etc. can be given, which is
analogous to that described for the scalar field in section 2. For the specific model (22),
and with similar weak-coupling and adiabatic approximations, the one-loop approximation to the
kinetic equation (59) is
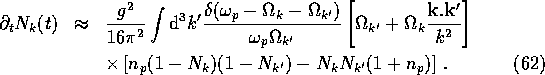
This does indeed have the form of a Boltzmann equation where, in the approximation described above,
the occupation-number changing processes are the decay of a scalar particle (momentum p=k+k', energy
, occupation number 
) into a pair of spin- particles (momenta k and k',
energies and 
, occupation numbers and 
) and the
inverse process of pair annihilation.