INSTITUTE FOR NUCLEAR THEORY
News
Home | Contact | Search | News archive | Site Map

|
INSTITUTE FOR NUCLEAR THEORY News Home | Contact | Search | News archive | Site Map |
|||||
Two-photon exchange and the proton form factor puzzle
The proton's electromagnetic form factors are one of the most basic
observables which characterize the proton's finite spatial extent.
One may have thought that with over half a century of measurements we
would know pretty much all that there is to know about the proton's
charge and magnetic form factors, at least in the kinematics accessible
to experiment. It was a great surprise, therefore, when several years
ago a new type of experiment revealed an unexpectedly different behavior
of the form factors than had previously been accepted.
For many years, the standard way to extract the electric and magnetic
form factors in elastic electron-proton scattering was via the
"Rosenbluth", or longitudinal-transverse (LT) separation method, by
analyzing the angular (θ) dependence of the cross section at
fixed momentum transfer squared, Q2. At the most backward scattering
angle (θ=180 degrees) the cross section depends only on the
magnetic form factor, GM, while from the slope in θ (or rather
the virtual photon polarization, ε, which depends on both
θ and Q2) one extracts the ratio of the electric to magnetic
form factors, GE /GM. These experiments found that the Q2
dependence of GE approximately follows that of GM, although the
experimental uncertainties in GE increase significantly at large
Q2.
Recent measurements at Jefferson Lab using the alternative, polarization
transfer (PT) technique have found a dramatically different behavior of
the ratio GE /GM compared with the Rosenbluth results [1], leading
to much discussion about the possible origin of the discrepancy. In
particular, the PT results reveal a linear drop in the ratio with Q2,
up to the largest available value of Q2 ≈ 6 GeV2. With its
considerably smaller systematic uncertainties, the PT method is believed
to be more reliable for extracting the form factor ratio, however,
experimental error in the LT measurements has also been ruled out as an
explanation.
To break the impasse, attention has subsequently turned to the
theoretical assumptions that go into the analysis of the data.
A likely candidate that has been identified is the two-photon exchange
process, shown in Fig. 1, which forms part of the electromagnetic
radiative corrections that must be applied to the raw data. While the
exchange of two photons gives corrections to both the LT and PT
measurements at the level of a few percent, because the LT method is
very sensitive to small variations in the θ dependence of the
cross section, two-photon effects have a dramatically larger impact on
the results from LT separation.
The first detailed calculations of the two-photon exchange amplitudes,
or more precisely their interference with the one-photon exchange or
Born amplitude, were made using a hadronic basis including nucleon and
Δ intermediate states [2]. These were also found to have a strong
angular dependence when the finite size of the nucleon was taken into
account, and had the correct sign and magnitude to resolve most of the
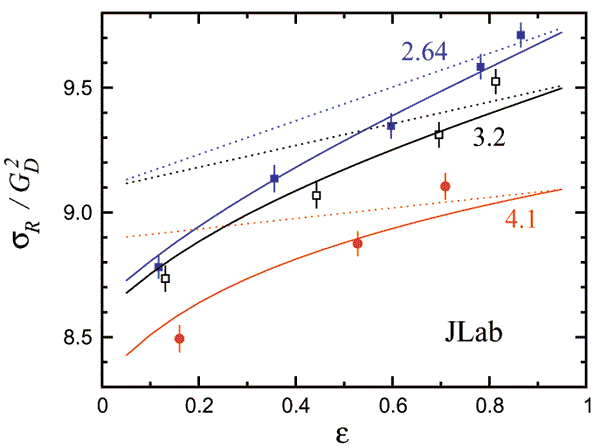
difference between the LT and PT measurements, as Fig. 2 illustrates.
In a complementary approach, two-photon contributions have also been
calculated at the partonic level, in terms of generalized parton
distributions [3]. These contributions, which parameterize the high-mass
part of the intermediate state (in contrast to the nucleon elastic and
Δ intermediate states) were also found to reduce the Rosenbluth
cross sections, bringing them closer to the PT results. Between the
various contributions, it is very likely that two-photon exchange
provides most, if not all, of the resolution of the form factor
discrepancy.
In the future it will be important to confirm the role of two-photon
exchange by measuring quantities that are directly sensitive to it.
One such observable is the ratio of positron-proton to electron-proton
elastic cross sections. The Born amplitude changes sign under the
interchange e − ↔ e+, while the two-photon exchange
amplitude does not. The interference of the one- and two-photon
exchange amplitudes therefore has the opposite sign for e − p and
e+ p scattering, which can show up in the experimental ratio.
Existing positron scattering data have large errors which preclude
any definitive conclusions, however, an experiment at Jefferson Lab
using a tertiary e+/e − beam (produced by passing bremsstrahlung
photons radiated from the primary electron beam through an e+/e −
converter) aims to place tight constraints on the two-photon exchange
amplitude up to Q2 ≈ 2 GeV2 [4]. A related experiment is
also being planned at the VEPP-3 storage ring in Novosibirsk [5].
The imaginary part of the two-photon exchange amplitude can also be
accessed by measuring the electron beam asymmetry for electrons
polarized normal to the scattering plane. Because this is forbidden
in the Born approximation, the normal polarization provides a clean
signature of two-photon exchange effects, and experiments at MIT-Bates
and MAMI have indeed observed non-zero asymmetries [6]. Knowledge of
the imaginary part of the two-photon exchange amplitude can be used to
constrain models of Compton scattering, although relating this to the
real part (which enters in the cross section measurements) requires more
detailed dispersion relation analysis.
What are the wider consequences of all this? Firstly, the new PT
measurements have prompted a serious rethinking of our understanding
of the distribution of charge in the proton (or more illustratively,
its "shape"). The new data have spawned numerous theoretical
speculations about the microscopic origin of the particular Q2
dependence of the electric and magnetic form factors, and progress is
being made towards understanding this behavior from first principles
through lattice QCD simulations. Applications of two-photon effects
have also found their way recently into atomic physics, in the study
of polarizability effects on hyperfine splitting in hydrogen [7].
More broadly, the critical role played by two-photon exchange in
elastic scattering has exposed the inherent limitations of the Born
approximation in nuclear physics, which has hitherto been a ubiquitous
tool with which to probe the structure of hadrons and nuclei.
The lesson learned is that even in QED - long thought to be well
understood and hence uninteresting - one cannot ignore the fact that
the proton has finite size.
Fig. 2:
Reduced Rosenbluth cross section σR (scaled by the dipole form
factor GD2) versus the virtual photon polarization ε for
several values of Q2: Q2 = 2.64 (filled squares), 3.2 (open squares)
and 4.1 GeV2 (filled circles) [from Qattan et al., Phys. Rev. Lett. 94,
142301 (2005)]. The dotted curves are Born cross sections evaluated
using form factors fitted to the PT data (hence they disagree with the
Rosenbluth cross sections), while the solid curves account for two-photon
contributions.
Reported by Wally Melnitchouk
March 16, 2007
![]()
References
Figures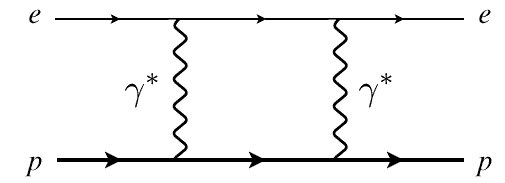
Fig. 1:
Two-photon exchange diagram for elastic electron-proton scattering.