Physics Results
Our lattice QCD
calculations were performed with Chroma , the lattice software written by Robert
Edwards and his team
at the Jefferson Laboratory (JLab). Chroma
contains all of the necessary packages to perform lattice
calculations. We have written all of the contraction code
required for two-particle interactions and single hadron ground-state
spectroscopy. We submitted a proposal for an exploratory study
of two-hadron interactions and for a partially-quenched calculation of
the nucleon mass (to extract the sigma-term and strong isospin
breaking) to the SciDAC Lattice committee, and were awarded roughly 8%
of the JLab computing resources for the funding period April 2005 to
April 2006. The LHP collaboration very kindly allowed us to use
the domain-wall propagators they had computed on the MILC lattices as
part of their program funded by SciDAC.
Pion-Pion Scattering in the I=2 Channel
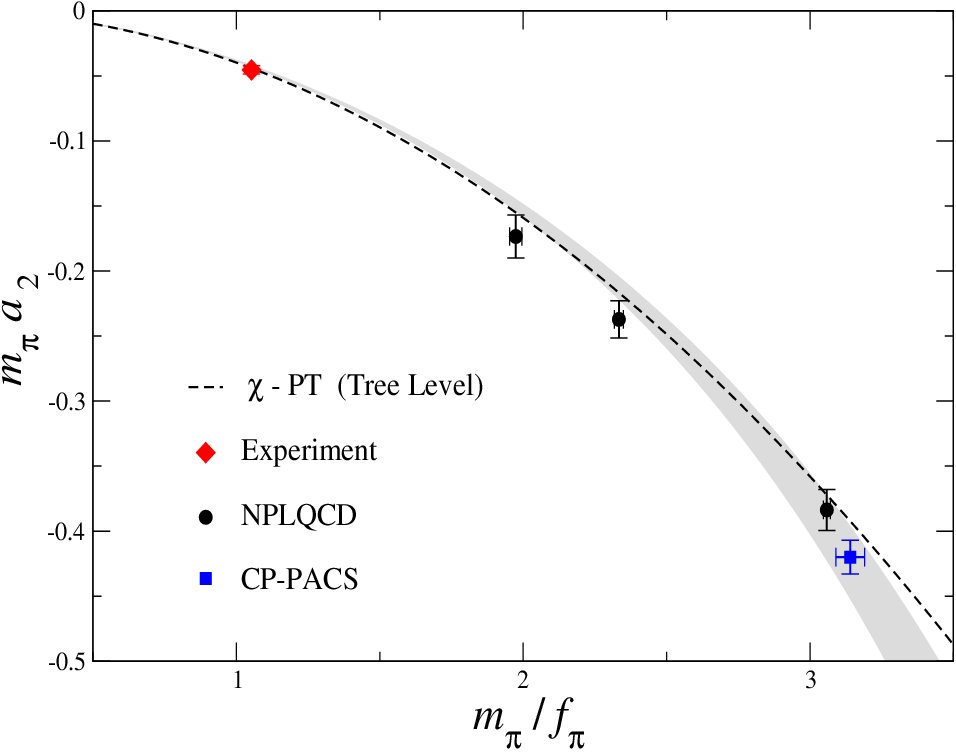
The
results of our calculation of pion-pion scattering in the I=2 channel
are shown in the above figure. The scattering length multiplied
by the pion mass is plotted vs the pion mass dividied by the pion
decay constant as measured on the lattices.
Both the quantities on the vertical and horizontal axes are independent
of the scale-setting procedure.
The lattice data was computed with domain-wall valence quarks (Kaplan
fermions) on the fully-dynamical gauge configurations with staggered
sea-quarks. The lattice spacing is b~0.125 fm, and the spatial
extent L~2.5 fm.
The blue-point is the lowest mass datum computed by the CP-PACS
collaboration with Wilson on Wilson quarks.
The dashed line corresponds to the parameter free tree-level prediction
of chiral perturbation theory (Weinberg), and is seen to be very close
to what is computed with lattice QCD. The shaded region
corresponds to our fit, and associated uncertainties, to chiral
perturbation theory at the one-loop level. Both the tree-level
and loop-level extrapolations to the physical point agree with the
experimental value, and have a smaller uncertainty.
Nucleon-Nucleon Scattering
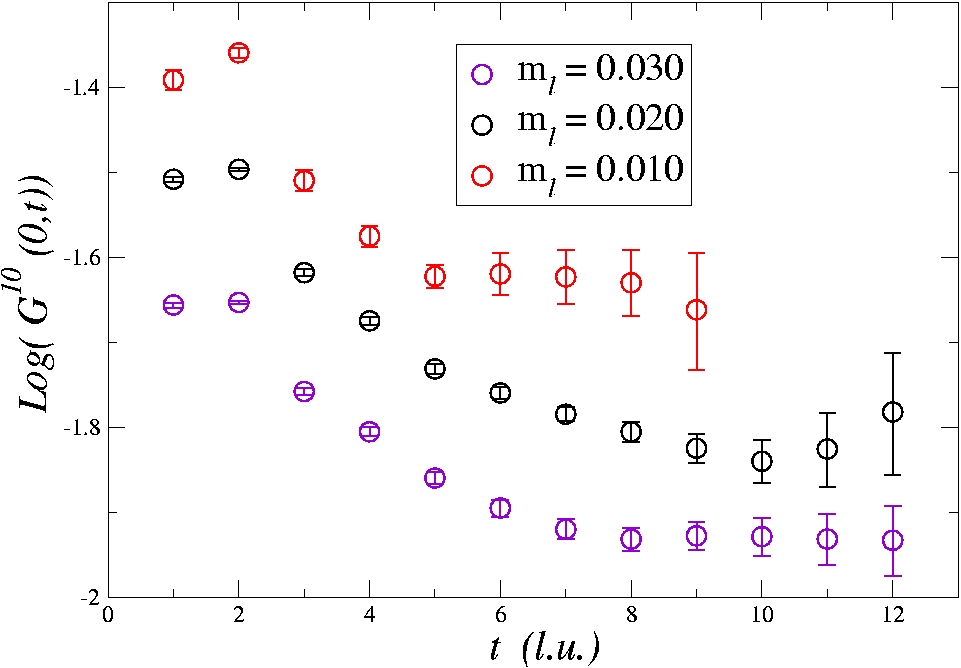
We have calulated
the energy shifts associated with two nucleons using domain wall valence quarks on the
staggered MILC lattices with b~0.125
fm, and spatial extent L~2.5 fm. The ratio of the
proton-proton correlator to the square of the single proton correlator
is shown below.
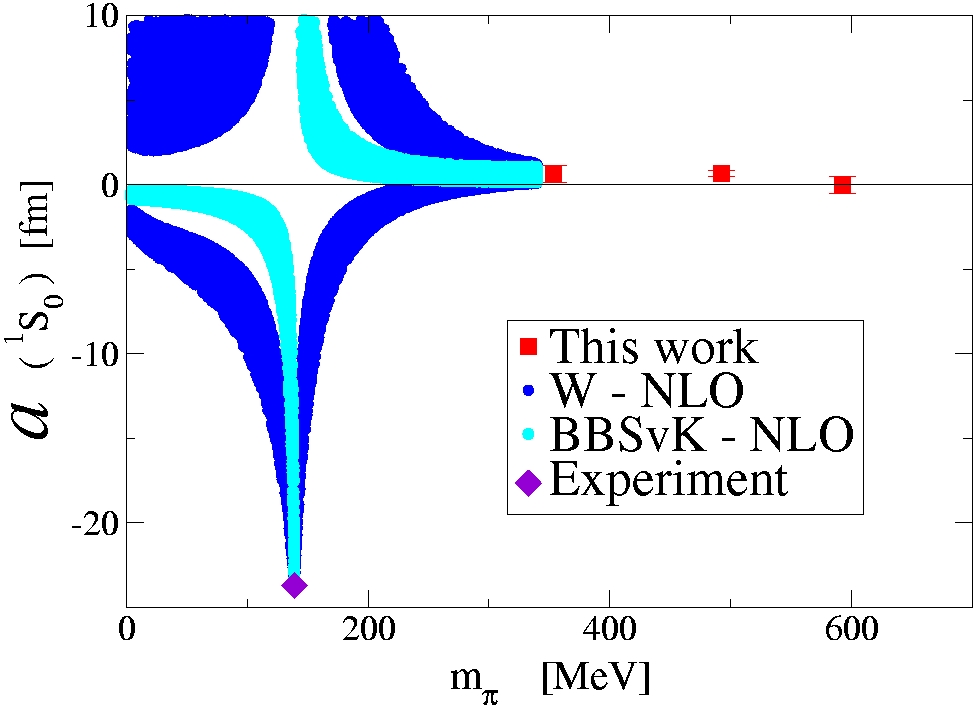
The scattering
lengths in the 1S0 channel extracted from the energy-splitting derived
from the ratio of correlators
are shown in the figure below, along with the currently best
theoretical understanding about how to extrapolate to the chiral
limit. In the extrapolation the experimental value of the
scattering length at the physical pion mass has been included, as
currently there is not enough lattice data in the regime where
the theory is valid.
The scattering
lengths in the 3S1-3D1 coupled-channel extracted from the
energy-splitting derived from the ratio of correlators
are shown in the figure below, along with the currently best
theoretical understanding about how to extrapolate to the chiral
limit. Again, in the extrapolation the experimental value
of the scattering
length at the physical pion mass has been included, as at this point in
time there is not enough lattice data in the regime where the theory is
valid.
The chiral
extrapolations were performed with the effective field theories (EFT)
that have been developed during the last 15 or so years, initiated by
the pioneering work of Weinberg. The advantage these theories
have over traditional approaches to nuclear physics is that the
dependence upon the light quark masses is explicit.
However, the lowest pion mass data point is at the upper limits
of applicability of the EFT's, and as such there is significant
uncertainty in the extrapolations. Clearly, a lattice QCD
calculation at a pion mass of ~ 250 MeV will dramatically reduce the
uncertainty.