The previous section has taught us that in general the orbital
angular momentum
of strongly interacting
states is not a conserved quantum number due to the presence of
non-central forces. These forces commute
with the total spin of the system and hence we can classify the
states by the ![]() and
and ![]() quantum numbers.
For example, the deuteron is a
quantum numbers.
For example, the deuteron is a ![]() object, with orbital angular
momentum being a mixture of
object, with orbital angular
momentum being a mixture of ![]() and
and
![]() .
It is therefore convenient to define states of good
.
It is therefore convenient to define states of good ![]() and
and
![]() which are linear combinations of the spatial and spin wavefunctions
with different
which are linear combinations of the spatial and spin wavefunctions
with different ![]() .
The wavefunction for a given system is then a sum
over these states of different
.
The wavefunction for a given system is then a sum
over these states of different ![]() .
For the deuteron, we need
.
For the deuteron, we need ![]() and
and ![]() for each
for each ![]() .
The
.
The
![]() by
by
We can now compute some angular matrix elements relevant to the deuteron.
In order to make progress we rewrite the ![]() operator in terms of
the total spin operator,
operator in terms of
the total spin operator, ![]() ,
,
![$\displaystyle = 2\left[
3\left( {1\over 2} S_+ (\hat r_x - i \hat r_y)\ +\
{1\over 2} S_- (\hat r_x + i \hat r_y)\ +\ S_z \hat r_z\right)^2 - S^2\right]
\ \ \ ,$](img27.gif) |
(4) |
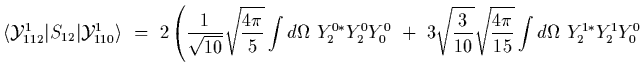 |
|||
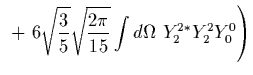 |
|||
| (5) |
| (6) |
Similar calculations lead to
| (7) |
The deuteron wavefunction ![]() (where
(where ![]() is the magnetic substate)
is a linear combination of
is the magnetic substate)
is a linear combination of ![]() and
and ![]() components
components
We recall that from our naive guestimates made previously,
the deuteron is a very extended object compared to
the range of the nuclear interaction. In the region outside
the potential, the coupled equations become
It is clear that solving the coupled equations is not going to be so easy.
In particular, we see that there
is the mixing angle ![]() that is apriori undetermined.
We see that for
that is apriori undetermined.
We see that for
![]() ,
the Swave wavefunction is uncoupled
from the D-wave admixture, but the D-wave
is infinitely coupled to the S-wave component.
We see that in order to solve these equations, we must compare with data,
so that the solution reproduce the
binding energy, magnetic moment and quadrupole moment of the deuteron.
,
the Swave wavefunction is uncoupled
from the D-wave admixture, but the D-wave
is infinitely coupled to the S-wave component.
We see that in order to solve these equations, we must compare with data,
so that the solution reproduce the
binding energy, magnetic moment and quadrupole moment of the deuteron.
In order for us to proceed, we therefore need to know how to relate these wavefunctions to the magnetic and quadrupole moments that are measured.