I hope that most of this is just a reminder to you of work
covered in other classes, hopefully the
introductory quantum lectures.
We are considering the situation of a wavepacket, localized
at -ve ![]() at time
at time
![]() .
We wish to form the (differential) cross section for this
wave packet to scatter off a scattering centre.
This amounts to determining the probability for the particle
in the wave packet to end up travelling at some
angle with respect to its initial direction.
Wave packets are inherently messy objects to deal with and so
it is more convenient to determine the
scattering amplitudes of incident plane waves, and the convolve
with the wavepacket amplitudes at the end.
In reality we never do this as the momentum spread of the wavepacket,
is small compared to other scales in
the problem.
.
We wish to form the (differential) cross section for this
wave packet to scatter off a scattering centre.
This amounts to determining the probability for the particle
in the wave packet to end up travelling at some
angle with respect to its initial direction.
Wave packets are inherently messy objects to deal with and so
it is more convenient to determine the
scattering amplitudes of incident plane waves, and the convolve
with the wavepacket amplitudes at the end.
In reality we never do this as the momentum spread of the wavepacket,
is small compared to other scales in
the problem.
When we are far from the scattering potential for a finite
range potential, then we know that the incident
wavefunction is just a plane wave ![]() ,
where
,
where
![]() where
where ![]() is the
reduced mass of the system.
As we are going to be dealing with scattering in states of
angular momentum
is the
reduced mass of the system.
As we are going to be dealing with scattering in states of
angular momentum ![]() it
is convenient to expand the incident plane wave in the
z-direction into angular momentum states
it
is convenient to expand the incident plane wave in the
z-direction into angular momentum states
It is obvious that this plane wave is a solution to the
schrodinger equation with no potential.
In order to determine the amplitude for scattering of this
incident plane wave we need to solve the
schrodinger equation with the complete potential ![]() (we are assuming a central potential).
We have that
(we are assuming a central potential).
We have that
If there was no potential ![]() everywhere, then the solution
to the schrodinger equation would be
everywhere, then the solution
to the schrodinger equation would be
![]() ,
where
,
where ![]() is a spherical Bessel function.
However, when there is a non-zero
potential, we can still have
is a spherical Bessel function.
However, when there is a non-zero
potential, we can still have ![]() vanish at the origin, while at
long distances (much larger than the range
of the potential) the solution has the form
vanish at the origin, while at
long distances (much larger than the range
of the potential) the solution has the form
It is useful to have the asymptotic forms of the Bessel and Neumann
functions explicitly to understand the
behaviour of the amplitudes
For a non-vanishing potential, we are free to define the ratio of
coefficients ![]() and
and ![]() to be
to be
We are now in a position to determine the cross section for a
given process.
We start by computing the flux of particles associated with
![]() .
From NR quantum mechanics we have that the current density is
.
From NR quantum mechanics we have that the current density is
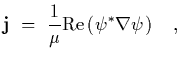 |
(14) |
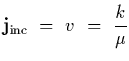 |
|||
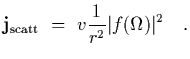 |
(15) |
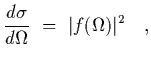 |
(16) |
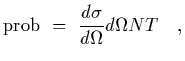 |
(17) |
Hence the cross section is