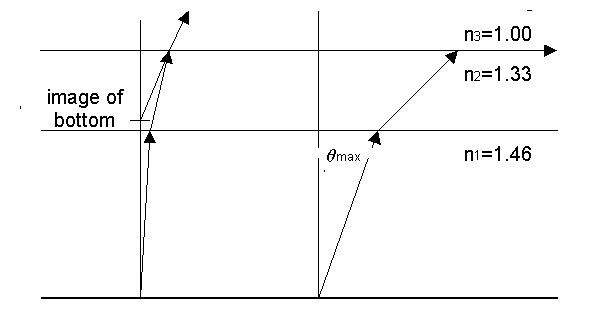
4. [25 points] A layer of water (n2=1.33) which is 2.0 cm thick floats on a thicker layer of carbon tetrachloride (n1=1.46) which is 4.0 cm thick. [Hint: in part (a) use the small-angle approximation with Snell's law.]

(a) [10 points] How far below the surface, viewed at normal incidence, does the bottom of the container appear to be, for light rays near normal incidence?
Method 1 (Ray Tracing): Let a ray from the bottom in the carbon tetrachloride move a vertical distance of t1, make an angle q1 with the vertical, and intercept the lower interface at x1. Then Tan q1 @ q1 = x1/t1. The angle in water is q2 and intercept the upper interface at x1 + x2, so Tan q2 @ q2 = x2/t2. From Snell's Law, n1 Sin q1 = n2 Sin q2 = n3 Sin q3 = Sin q3 (since n3=1), so from the small angle approximation q3 @ n1 q1. Extrapolating the final ray back to the perpendicular gives the apparent depth h', which is related to the other variables by Tan q3 @ q3 = (x1+x2)/h' or h' = (x1+x2)/q3 = (t1q1 + t2q2)/ n1 q1 = q1(t1 + (n1/n2)t2)/n1 q1 = t1/n1 + t2/n2 = (4 cm)/1.46 + (2 cm)/1.33 = 4.24 cm.
Method 2 (Refractive Interface Imaging):
The interface equation is n1/o + n2/i = (n2-n1)/r.
Since the interfaces are flat, the radius of curvature r is infinite and
we can write i = -o(n2/n1). Then the image
of the bottom at the lower interface is i1 = -o1(n2/n1)
= -(4 cm)(1.33/1.46) = -3.64 cm. This becomes the object for the
upper interface, i.e. o2 = t2 - i1 = 2
cm + 3.64 cm = 5.64 cm. The image of this second object is then i2
= -o2(n3/n2) = -(5.64)(1.00/1.33) = -4.24
cm. Thus the bottom appears to be 4.24 cm below
the upper interface.
(b) [10 points] A ray of light leaves the bottom of the container and emerges into the air above. What is the largest angle this ray can make with the perpendicular in the lower medium.
The emerging light at maximum angle travels along the surface of the water at an angle of 90o, so the angle in the water is the critical angle for total internal reflection Sin qc = n3/n2. The angle q1 below the lower interface can then be obtained from Snell's Law, i.e., n1Sin q1 = n2Sin qc = n2(n3/n2) = n3= 1.0. Therefore, the largest angle this ray can make with the perpendicular in the lower medium is q1 = ArcSin(1/n1) = ArcSin(1/1.46) = 43.23o.
(c) [5 points] Draw on the diagram above showing the paths of light rays from the bottom to illustrate both of your calculations. You may exaggerate the angles to illustrate your point.
(See diagram above)