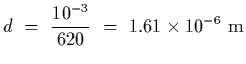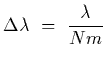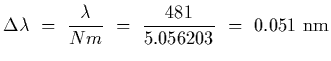

Next: Chapter 47: Problem 25
Up: Waves and Optics, Solutions
Previous: Chapter 47: Problem 19
Question: A grating has
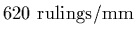 and is
and is
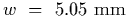 wide.
(a) What is the smallest wavelength interval that can be resolved in the third
order at
wide.
(a) What is the smallest wavelength interval that can be resolved in the third
order at
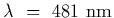 .
(b) How many higher orders can be seen?
.
(b) How many higher orders can be seen?
Solution:
The adjacent slit seperation is
In order to resolve two wavelengths we require that
where m is the order and N is the total number of lines on the grating.
Hence
Since
and
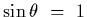 for the maximum order, we have that
for the maximum order, we have that
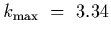 ,
and hence the third order is the highest that can be
seen.
,
and hence the third order is the highest that can be
seen.


Next: Chapter 47: Problem 25
Up: Waves and Optics, Solutions
Previous: Chapter 47: Problem 19
Martin Savage
1999-03-03
![]() and is
and is
![]() wide.
(a) What is the smallest wavelength interval that can be resolved in the third
order at
wide.
(a) What is the smallest wavelength interval that can be resolved in the third
order at
![]() .
(b) How many higher orders can be seen?
.
(b) How many higher orders can be seen?