

Next: Chapter 47: Problem 13
Up: Waves and Optics, Solutions
Previous: Chapter 47: Problem 2
Question: Light of wavelength
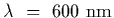 is incident
normally on a diffraction grating.
Two adjacent principle maximia occur at
is incident
normally on a diffraction grating.
Two adjacent principle maximia occur at
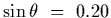 and
and
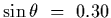 .
The fourth order is missing.
.
The fourth order is missing.
- 1.
- What is the seperation between adjacent slits?
- 2.
- What is the smallest possible slit width?
- 3.
- Name all the orders actually appearing on the screen with the
values derived in parts (a) and (b).
Solution:
Firstly, we can figure out the order of the intereference fringes from
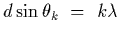 ,
and taking the ratio of two adjacent maxima gives
,
and taking the ratio of two adjacent maxima gives
from which we conclude k = 2.
Given, this we then can determine the seperation between adjacent slits to be
We can determine the angular position of the fourth order fronge to be
and hence
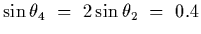 .
Now since the fourth order interference fringe is missing, we know that we have
a diffraction minima at that angular position.
Therefore, the minimum slit width that could give rise to a missing fourth
interference fringe is when the first diffraction minimum is at that location,
.
Now since the fourth order interference fringe is missing, we know that we have
a diffraction minima at that angular position.
Therefore, the minimum slit width that could give rise to a missing fourth
interference fringe is when the first diffraction minimum is at that location,
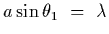 ,
and hence
,
and hence
The highest order interference fringe occurs at
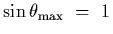 ,
and
thus
,
and
thus
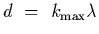 ,
from which we now can determine
,
from which we now can determine
 .
Given that the 4th fringe is absent, therefore, there is also a diffraction
minimum located precisely at the 8th fringe also.
Hence, present are interference fringes
1,2,3,5,6,7,9,10.
.
Given that the 4th fringe is absent, therefore, there is also a diffraction
minimum located precisely at the 8th fringe also.
Hence, present are interference fringes
1,2,3,5,6,7,9,10.

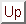

Next: Chapter 47: Problem 13
Up: Waves and Optics, Solutions
Previous: Chapter 47: Problem 2
Martin Savage
1999-03-03
![]() is incident
normally on a diffraction grating.
Two adjacent principle maximia occur at
is incident
normally on a diffraction grating.
Two adjacent principle maximia occur at
![]() and
and
![]() .
The fourth order is missing.
.
The fourth order is missing.
![]() ,
and taking the ratio of two adjacent maxima gives
,
and taking the ratio of two adjacent maxima gives
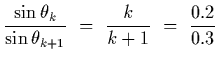
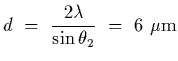
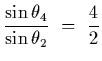
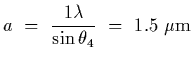
![]() ,
and
thus
,
and
thus
![]() ,
from which we now can determine
,
from which we now can determine
![]() .
Given that the 4th fringe is absent, therefore, there is also a diffraction
minimum located precisely at the 8th fringe also.
Hence, present are interference fringes
1,2,3,5,6,7,9,10.
.
Given that the 4th fringe is absent, therefore, there is also a diffraction
minimum located precisely at the 8th fringe also.
Hence, present are interference fringes
1,2,3,5,6,7,9,10.