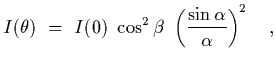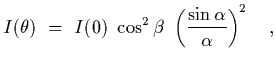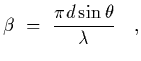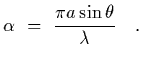

Next: About this document ...
Up: Waves and Optics, Solutions
Previous: Chapter 46: Problem 26
Question: Suppose that, as in sample problem 7 (Capter 46) the envelope
of the central peak contains 11 fringes. How many fringes lie between the
first and second minima of the envelope?
Solution: The general expressin for the intensity pattern for two slits
of width a and separation d is
where
and
If there are 11 fringes, then we know that the interference fringes
(corresponding to
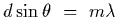 )
for
)
for
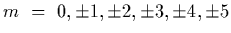 all lie in the diffraction central maximum.
Therefore, we know that the intereference fringes corresponding to
m = +6, +7, +8, +9, +10, (or alternately
m = -6, -7, -8, -9, -10)
will lie between the first and second diffraction minima.
Thus we have 5 fringes.
all lie in the diffraction central maximum.
Therefore, we know that the intereference fringes corresponding to
m = +6, +7, +8, +9, +10, (or alternately
m = -6, -7, -8, -9, -10)
will lie between the first and second diffraction minima.
Thus we have 5 fringes.


Next: About this document ...
Up: Waves and Optics, Solutions
Previous: Chapter 46: Problem 26
Martin Savage
1999-02-24