Chapter 46: Problem 12

Question: If you double the width of a single slit, the intensity pattern of the central maximum of the diffraction pattern increases by a factor of four, even though the energy passing through the slit only doubles. Explain this quantitatively.

Solution: Firstly, in the forward direction and in the Fraunhofer limit, the electric vectors from each point on the wavefront passing through the slit add up,

$${\bf E}_{\rm tot}~=~\sum_i {\bf E}_i \ \ \ ,$$

and so if the width of the slit is doubled, then ${\bf E}_{\rm tot}$ is doubled and the intensity is increased by a factor of four, since $I\propto \vert{\bf E}_{\rm tot}\vert^2$.

Secondly, the energy passing through the slit per unit time is equal to the intensity of the incident plane wave times the area of the slit. Thus, if the width of the slit is doubled, the energy passing through the slit is doubled.

Now the question is, how can these two true statements be consistent. Well, if the look at the diffraction pattern, you will notice that the width of the central diffraction maximum, maybe defined to be the location where

$$\left({\sin\alpha\over\alpha}\right)^2~=~{1\over 2} \ \ \ ,$$

which occurs when $\alpha~=~\sqrt{2}\sin\alpha$, where $\alpha$ is defined by

$$\alpha~=~{\pi a\sin\theta\over\lambda} \ \ \ ,$$

On page 975, the solution is found to be $\alpha~=~1.39156$. So for small $\theta$, we find that $\theta\sim{1\over a}$.

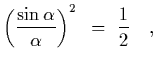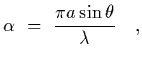The total energy in the central maximum is proportional to the intensity at $\theta~=~0$, times the width of the central maximum. By increasing the slit width by a factor of 2, the intensity at $\theta~=~0$ is increased by a factor of 4, but the width is decreased by a factor of 2, and so the total energy on the diffraction pattern is increased by a factor of 2 also.