Question: In a double slit experiment the distance between the slits is
![]() and the slits are
and the slits are
![]() from the screen.
Two interference patterns can be seen on the screen, one due to the light of
wavelength
from the screen.
Two interference patterns can be seen on the screen, one due to the light of
wavelength
![]() ,
and the other due to light of wavelength
,
and the other due to light of wavelength
![]() .
Find the separation on the screen between the
third-order interference fringes of the two different patterns.
.
Find the separation on the screen between the
third-order interference fringes of the two different patterns.
Solution: As the angle of the first many interference fringes is small,
we can use the small angle limits of all the trig functions.
![]() ,
and
,
and
![]() ,
where the superscript on
,
where the superscript on ![]() denotes that it is associated with that
particular wavelength, and the subscript denotes the order of the fringe.
We use the fact that the distance from the forward direction to the fringe is
given by
denotes that it is associated with that
particular wavelength, and the subscript denotes the order of the fringe.
We use the fact that the distance from the forward direction to the fringe is
given by
![]() .
Thus the difference between the two third order fringes is
.
Thus the difference between the two third order fringes is
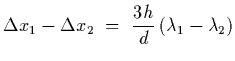 |