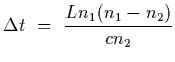Chapter 43: Problem 49

Question: In an optical fibre, different rays traveldifferent paths along the fibre, leading to different travel times. This causes a light pulse to spread out as it travels along the fibre, resulting in information loss. The delay time should be minimized in designing a fibre. Consider a ray that travels a distance L along a fibre axis and another that is reflected at the critical angle, as it travels to the same destination as the first.

1.

Show that the diference $\Delta t$ in the time of arrival is given by

$$\Delta t~=~{L n_1 (n_1-n_2)\over c n_2}$$

where n₁ is the index of refraction of the core and n₂ is the index of refraction of the cladding.

2.

Evaluate $\Delta t$ for the fibre in Problem 48 (Chap 43) with $L=350~{\rm km}$

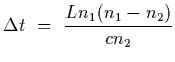Solution: The path difference between travelling down the axis and travelling at an angle $\phi$ is

$$\Delta x~=~L\left( {1\over\sin\phi}-1\right)$$

where $\phi$ is measured wrt the normal of the outer cladding. Snells law tells us that for total internal reflection at the cladding, we have that $n_1\sin\phi~=~n_2$, this we have that

$$\Delta x~=~L\left( {n_1\over n_2}-1\right)$$

and hence a time difference of

$$\Delta t~=~{L\over v}\left( {n_1-n_2\over n_2}\right)$$

where the speed of light in the fibre is $v={c\over n_1}$, leading to

$$\Delta t~=~{L n_1\over c}\left( {n_1-n_2\over n_2}\right)$$

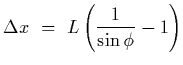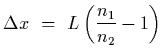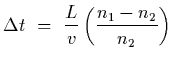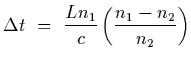For n₁=1.58, n₂=1.53 and $L=350~{\rm km}$, we have that $\Delta t~=~6.03\times 10^{-5}~{\rm s}$.