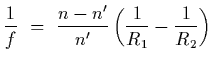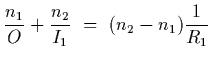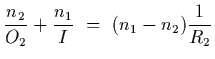

Next: Chapter 44: Problem 22
Up: Waves and Optics, Solutions
Previous: Chapter 44: Problem 12
Question: Show that the focal length for a thin lens whose index of
refraction is n and which is immersed in a fluid whose index of refraction is
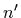 is given by
is given by
Solution:
Starting with the relation between object and image for one spherical surface,
we have that
where I1 is the image from the curved surface, which serves as the object
for the second curved surface. Taking into account the -ve sign due to the
location of the image, we have that the object for the second surface is
O2=-I1.
For the second surface, we have that
The answer follows.
Martin Savage
1999-02-10
![]() is given by
is given by