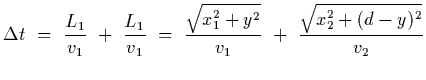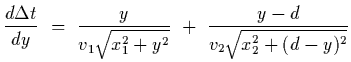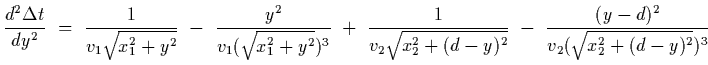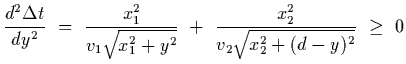

Next: Chapter 43: Problem 41
Up: Waves and Optics, Solutions
Previous: Waves and Optics, Solutions
Question: Prove that the optical path lengths for reflection and
refraction in Figs 10 and 17 (Chap 43) are each a minimum when compared with
other nearby paths connecting the same two points.
(HINT: Examine the quantity
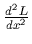 .
.
Solution: For refraction we have that the time required for light to
travel from point 1 to point 2 a particular path is
The first derivative wrt y is
This leads to Snells law of refraction (assuming a minimum for 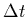 ).
The second derivative of
).
The second derivative of 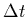 is
is
Since
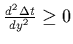 for all values of y we see that Snells
law corresponds to a global minimum for the time required for the light to
propagate from 1 to 2.
The reflection relation can be found trivially by setting v1=v2.
for all values of y we see that Snells
law corresponds to a global minimum for the time required for the light to
propagate from 1 to 2.
The reflection relation can be found trivially by setting v1=v2.


Next: Chapter 43: Problem 41
Up: Waves and Optics, Solutions
Previous: Waves and Optics, Solutions
Martin Savage
1999-02-10
![]() .
.