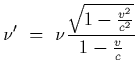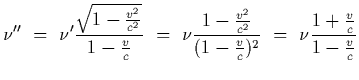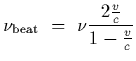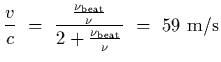

Next: Chapter 43: Problem 3
Up: Waves and Optics, Solutions
Previous: Chapter 42: Problem 14
Question: Microwave, which travel at the speed of light, are reflected
from a distant airplane approaching the wave source. It is found that when the
reflected waves are beat against the waves radiating from the source the beat
frequency is
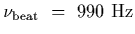 .
If the microwaves have wavelength
.
If the microwaves have wavelength
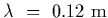 ,
what is the
approach speed of the plane?
,
what is the
approach speed of the plane?
Solution: The approaching aircraft sees microwaves of frequency
which is the frequency of the microwaves reflected back toward the source.
Therefore the source sees reflected microwaves of frequency
The beat frequency is the difference
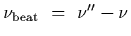 ,
which is
,
which is
leading to


Next: Chapter 43: Problem 3
Up: Waves and Optics, Solutions
Previous: Chapter 42: Problem 14
Martin Savage
1999-02-03
![]() .
If the microwaves have wavelength
.
If the microwaves have wavelength
![]() ,
what is the
approach speed of the plane?
,
what is the
approach speed of the plane?