Question: Light of wavelength
![]() in a vacuum
travels
in a vacuum
travels
![]() in a medium of refractive index n = 1.51.
Find the wavelength in the medium, the optical path length and the phase
difference after moving that distance wrt light traveling the same distance in
a vacuum.
in a medium of refractive index n = 1.51.
Find the wavelength in the medium, the optical path length and the phase
difference after moving that distance wrt light traveling the same distance in
a vacuum.
Solution: The frequency in the medium is the same as in the vacuum, and
so the wavelength must be reduced by the ratio of speeds, hence
![]() .
The optical path is the distance the light would have traveled in the time it
took to travel the distance in the medium. Therefore, it is simply the
distance traveled in the medium, multipled by the ratio of refractive indices,
.
The optical path is the distance the light would have traveled in the time it
took to travel the distance in the medium. Therefore, it is simply the
distance traveled in the medium, multipled by the ratio of refractive indices,
![]() .
The phase difference upon after traveling dis
.
The phase difference upon after traveling dis
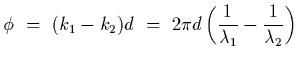 |