Chapter 20: Problem 54

Question:        A source S generates circular waves on the surface of a lake, the pattern of wave crests being shown in fig. 25 (chap 20). The speed of the waves is $c = 5.5\ {\rm m/s}$ and the crest-to-crest separation is $\lambda = 2.3\ {\rm m}$. You are in small boat heading directly toward S at a constant speed of $v = 3.3\ {\rm m/s}$ with respect to the shore. What frequency of waves do you observe?

Solution:        

The source is at rest and the observer is moving, therefore we have

$$\nu \nu_0\left( 1 + {v\over c}\right)\ \ = \ \left({c\over\lambda}\right) \left( 1 + {v\over c}\right)$$ =

$${5.5\over 2.3}\left( 1 + {3.3\over 5.5}\right)$$ =

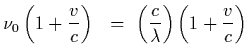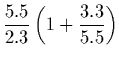$$3.82\ {\rm Hz} \ \ \ .$$ = (10)