Foam Modeling
By: Arend van der Zande
Advisor: Jerry Seidler
Introduction:
In this paper I discuss the research concerning foams currently being done by the Micro-Structural Kinetics group in the University of Washington and the small part I had to play in the research. Specifically, I was involved in the modeling of the statistical properties of foams, and using the statistical properties to develop a methodology for reconstructing foams.
What are Foams?
Foams are a common part of everyday life. The general definition of a foam is a Cellular solid. In other words, foams are two materials which mix by generating bubbles and structure surrounding them in a variety of different ways. The basic structure of the foam is as follows. A foam is composed of bubbles of one material mixed into another material. If the density of the bubbles (usually called Cells) is such that no two bubbles are close to touching each other, the bubbles will be round and there is very little structure to be described. However, when the density of bubbles gets higher, then bubbles will begin to be very close to each other. When this is the case, there is a small amount of material left in between the two bubbles. This is called the cell wall. At higher densities more and more bubbles come into contact. The juncture where cell walls meet is called a Strut. The juncture where different struts meet is called a vertex.
Foams generally fall into two classes, Solid foams and Liquid foams. Solid foams are foams which have hardened structure which does not change over time unless put into extreme conditions. Liquid foams are foams which undergo the process of coarsening. Coarsening is where bubbles in the material exchange material, causing them to change size and, in effect, the overall structure of the foam over time.
Some common examples
of foams include:
Liquid Foams:
- Beer Froth (always a favorite example)
- Soap Bubbles
Solid Foams:
- Cake
- Bike Helmets
- Cancelous Bone
- Wood
- Most padding in chairs
Why Study Foams?
Despite the fact that foams are a ubiquitous part of our lives, they are not very well understood. There is no way to predict what a foams properties will be without testing them. Currently, there are hundreds of processes by which foams can be made, each resulting in different structure with different materials. However, it is largely a cookbook process by which new foams are developed in for resulting properties. Basically, there is no understanding of how micro-structural disorder plays a role in the macroscale effects, though all research up until now suggests that there is a great deal of influence.
In addition, from a physics perspective, foams are a very special system for studying Non-equilibrium Statistical Mechanics. The reason, is that foams are a system about which it is possible to have all of the information. It is possible to know the structure of the Foam down to a very fine detail, and it is possible to measure the properties of the foam. All that is left is to find a way to connect the two pieces of information together.
Current Group
Research:
In the previous section, I mentioned that it is possible to get all of the information about foams. This is a true statement, but except for some special systems, we do not generally know the exact structure of most foams, mostly because it is hard to look at them. In addition, the exact structure of two foams made by exactly the same manufacturing process (i.e. foams of the same type) will not have exactly the same structure, simply because the manufacturing process is chaotic. Hopefully, however, two foams of the same type will share the same micro-structural statistics. Properties on the other hand are relatively easy to measure and most foams are fully understood in this way.
The First order of research was to develop a method for imaging the exact structure of foams, and to use this information to find the micro-structural statistics of the foam. In order to do this, the Group developed a method for imaging structures using x-ray micro-tomography building off of previous research into imaging sand piles. This method takes a 3D picture of the foam sample. Next, using image recognition software, the structure of the foam is identified from the picture. The various struts and vertices of the foam and how they connect together are recognized and cataloged and the foam has been fully reconstructed on the computer.
Once this is done, one can make measurements on the statistics of the real foam. For example, the length of struts can be measured and put into a distribution. Ideally, soon simulations based on these real foam statistics to predict properties of foams will be put into action.
In addition to using the information to try to connect microstructure with the properties of foams, any imaging data and statistics that we derive will be put up on a webpage for others to use in their own research.
My Research:
My part in the rather large and lengthy project has been to look at the statistics inherent in a foam to decide whether it is possible to model foams. With this in mind, I have done the following. Using a simple system, I have developed and tested different statistical representations of microstructure. I am comparing the different distributions to try to find out which ones we need to fully describe the system. In addition, I am developing computational reconstructions which, given a distribution describing the system, how completely does it define other distributions in the system. These reconstructions are being made to see if it is possible to generate an entire foam with all of the expected macro-scale properties given its micro-structural properties, and which pieces of information are needed in order to make this happen.
The long range goal of these simulations is to relate the properties of a system with the statistical structure. If this connection can be made, then it might be possible to generate foams with a given set of properties.
The System:
We used a very simple system that is well studied to model so that we could compare our initial results with the results of others and be sure that we are on the right track. The system that we used was the two dimensional Delaunay-Voronoi Tessellation. In this system, for a given set of seed points thrown down randomly in a plane, the cells are all of the points which are closer to a particular seed point than to any other seed point in the system. The edges are the points which are equally close to two seed points and the vertices are equally close to three seed points.
Despite the simplicity of the system, it actually is a good representation for a physical system. It accurately describes the structure of a two dimensional soap foam. The way such a foam is constructed is by taking two slabs of material and putting them very close together. By blowing bubbles of larger diameter than the separation of the slabs, one can generate “flat” bubbles in between the plates. If the density of bubbles is high, they will arrange themselves in a pattern consistent with the voronoi tessellation.
The Delaunay Triangulation is completely analogous to the Voronoi Tessellation. The Delaunay Triangulation forms lines between a seed point and each of its nearest neighbor seed points, forming triangles. Nearest neighbor seed points are completely equivalent to points which share a cell edge, hence the two tessellations are equivalent. In order to maximize data and not have issues with the edges, we used periodic boundary conditions.
In order to calculate the Delaunay-Voronoi Tessellation, we used the C program QHULL, and qh-Math to port the QHULL into Mathematica.
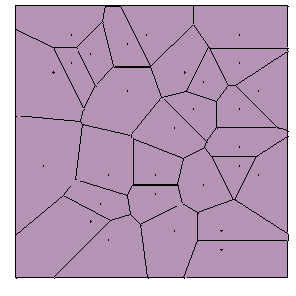
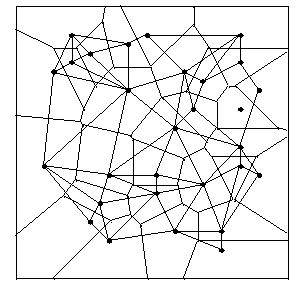
Figure 1:
a) Picture of the Voronoi Tessellation alone for a random set of 30 seed points without periodic boundary conditions.
b) Picture of the same Voronoi Tessellation with the Delaunay Triangulation for the same points overlapping.
How to describe the
system?
The following are a list of the different distributions that were calculated to measure/describe the microstructure of the Delaunay-Voronoi Tessellation.
a) Cell Edge Length Distribution: The cell wall lengths play a large role in the structure of a material.
b) Nearest Neighbor Distribution: This is the distribution of lengths of the Delaunay triangle sides. It is a measure of the distance which cells are separated by. It is an alternate description to the Cell Edge Length Distribution.
c) Second Nearest Neighbor Distribution: The exact length and position of a cell wall is not determined by separation of two points alone. The endpoints of a cell wall are determined by points which are further away from the original point. Points which share a connecting edge of two Delaunay triangles but are not on the edge themselves are second nearest neighbors. This is equivalent to them affecting only the endpoints of a cell edge.
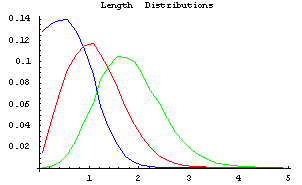
Figure 2:
On this graph the three length distributions are shown together. The horizontal axis is a length scale which has been scaled so that 1 is the characteristic length of the system 1/(n)^.5 where n=30,000 points in this graph. The vertical axis is the probability density of being at a particular length. Blue is the Cell Edge Length Distribution, Red is the Nearest Neighbor Distribution, Green is the Second Nearest Neighbor Distribution.
d) Angular Distribution: The angles made by two edges meeting at a vertex. This distribution was derived theoretically by R.E. Miles, so we were able to compare our results against a theoretical distribution.
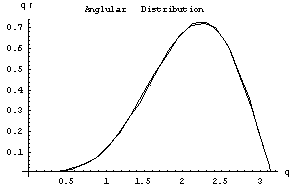
Figure 3: The Theoretical and Angular distributions for 30,000 seed points. The distributions converge rather nicely as n increases. The horizontal axis is the angle from 0 to pi. The vertical axis is the probability density.
Reconstructions:
Using the distributions derived from the Delaunay-Voronoi Tessellation, we tried to derive the other distributions computationally, to see how much information is shared between them. The different Reconstructions are as follows:
a) Using the nearest neighbor distribution, we tried to reconstruct the second nearest neighbor distribution. We did this by selecting five lengths from our nearest neighbor distribution. If possible, we constructed two triangles using the five lengths and measured the distance between the two points not sharing the side. If the distance between the two points was greater than the shared side length, we accepted the distribution. The result of this distribution was not very good, because the probability of being able to construct a triangle with the shorter lengths mixed with longer lengths was not so good. To try to fix the problem, we set up an ensemble selection method, where if a set of lengths generated a triangle, the probability of getting those lengths again is reduced. This helped the problem but did not fix it entirely.
b) Next we reconstructed the Angular distribution using the Nearest Neighbor Distribution. We used the same selection techniques as for the previous reconstruction as well as selecting from the joint distribution of three lengths.
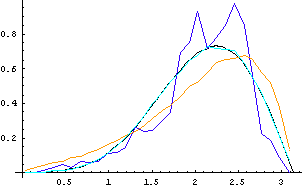
Figure 4:
The angular reconstructions for 10000 seed points. Black is the theoretical distribution. Blue is the distribution reconstruction which is to narrow and jumpy for even large numbers of points. Yellow is the ensemble reconstruction which smoothes out nicely, but is too wide. Light blue is the joint nearest neighbor distribution reconstruction which converges to the theoretical distribution. This is not surprising because we used an algorithm similar to the joint distribution to generate our points in the first place.
The next question that needs to be asked of reconstructions is whether or not it is possible to fit micro-structures together to make a macrostructure.
Information Theory:
Information theory is a branch of mathematics which formally describes how much is known about a system and how much two distributions in the system share information. This theory gives us a formal way to figure out how much information we need to fully describe a foam.
Another application is that Information gives us a method for calculating the entropy of a system. This gives us a good way to describe the disorder of the system.
Conclusion:
The main focus of this research project is to develop a method for using micro-structural statistics to reconstruct a macroscopic system. Once we have developed an algorithm for reconstruction of the Delaunay-Voronoi Tessellation, we can generalize the results to work on real foams. This will provide a significant step in the process of modeling of real foams.
Many Thanks to the following people/institutions:
v My advisor Gerald Seidler
v The other members of the Microstructural Kinetics Laboratory. For cool movies, advice, and good company.
§ Erin “Hardcore Hardware” Behne
§ Yejun “Graph King” Feng
§ David “Night Shift” Wells
§ Noah “Movie Man” Giansiracusa
§ Brandon “What’s That Your Playing?” Chapman
v The UW Physics REU Staff
v The National Science Foundation for providing free money, food, housing, entertainment, and travel for something that I would have jumped at the chance to do for no reimbursement whatsoever but would not have been able to afford.
v Ian’s Domain for many meals of inedible food.
v The other REU students for being the coolest group of people I have ever had the honor of hanging out with.