The Phases of Dense Matter (INT-16-2b)
(INT Program July 11 - August 12, 2016)
Reported by Mark Alford, Pawel Danielewicz, Chuck Horowitz, Thomas Schaefer
Date posted September 19, 2016
Scientific goals and achievements of the program INT 16-2b "The phases of dense matter"
One of the central aims of nuclear and particle physics is to understand the phases of matter that exist under extreme conditions of high density and/or high temperature. This program focused on inferring the properties and phase structure of dense matter from both laboratory experiments and astronomical observations.
The program brought together a number of communities including those working on dense QCD, lattice QCD, heavy-ion collisions, radioactive-beam experiments at a range of energies, and the communities concentrating on the structure and evolution of neutron stars.
Program goals included:
- clarifying our knowledge of the QCD phase diagram
- emphasizing the need for a consistent many-body description of equilibrium and transport properties probed by laboratory experiments and astrophysical observations,
- tightening connections between particular laboratory and astronomical observables and the properties of dense matter
- improving communication among nuclear physicists and astrophysicists.
The program yielded the following prospects for future progress:
Electromagnetic astronomy:
-
The observations of two solar mass neutron stars have provided strong constraints on theoretical descriptions of the equation of state and other properties of dense matter, and indicate that the speed of sound squared rises above 1/3 near a few times nuclear saturation density (n_sat). If future observations can give an increased limit on the maximum mass, this will give even more stringent constraints.
-
Observations of neutron star radii will provide valuable further constraints, but just from the two-solar-mass constraint, causality (speed of sound less than speed of light), and assumptions about the equation of state below nuclear density, we can say that the typical radius will be 10 to 13 km. This radius constraint can be improved with further x-ray observations including the x-ray timing mission NICER.
-
More measurements of neutron star temperatures and ages would clarify whether their cooling can be explained in terms of modified Urca processes in conventional nuclear matter. If some show faster cooling, the explanation would require invoking exotic processes and perhaps exotic phases.
-
Apparent stability of rapidly rotating neutron stars against r-mode oscillations suggests unconventional damping mechanisms, possibly involving exotic phases. More accurate temperature measurements of isolated neutron stars will help us estimate the r-mode saturation amplitude (if any).
Gravitational wave astronomy:
-
Gravitational waves from neutron star mergers, once observed, may contain signatures of the phase structure of matter at densities up to a few times n_sat and temperatures up to 100 MeV. In addition GW observations with high signal to noise can constrain the neutron star radius and dipole polarizability.
Accelerator experiments:
Heavy ion collisions could find the chiral critical point via a beam energy scan; collisions with E/A less than or of order a GeV show no sign of any strong first order phase transition in symmetric matter at densities up to about 3 n_sat.
The "symmetry energy" can be probed at subsaturation to moderately suprasaturation densities (up to about 2 n_sat) using heavy ion collisions and nuclear structure observables. The variation of the symmetry energy with density can be probed via parity violating electron scattering measurement of neutron skin thickness, although at present the statistical errors large.
Fundamental theory:
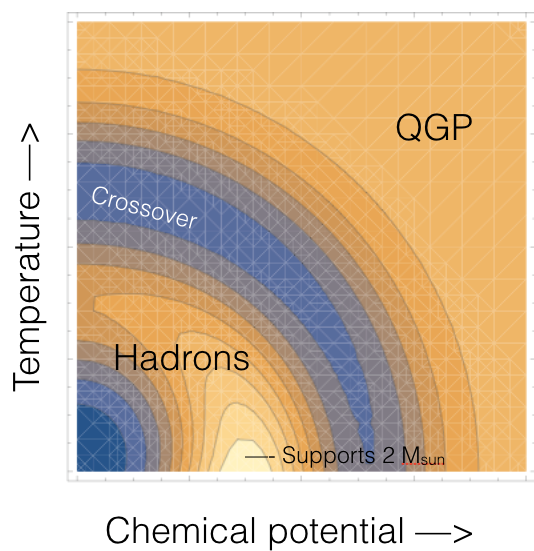
Schematic of speed of sound of dense matter:
The figure below is a cartoon of the speed of sound squared in dense matter as a function of temperature and density. At low densities, as studied at RHIC and the LHC, the speed of sound first rises with temperature and then falls to a local minimum near the crossover from hadronic matter to a quark gluon plasma. As the temperature rises further, the speed of sound squared approaches 1/3 c^2 from below. A similar pattern is expected for the dependence of the speed of sound on density at low temperature. The global maximum in the speed of sound squared, at a value near to and possibly above 1/3, likely occurs somewhat above nuclear density, at low temperature. This maximum is necessary to support two solar mass neutron stars against collapse to a black hole.
Caption: Minimal structure of the speed of sound squared in nuclear matter as a function of baryon chemical potential and temperature (arbitrary units). Higher values are in light orange, lower values in dark blue.
|