By far, the most common approaches today to understanding the structure of atomic nuclei are femtoscopic, by which is meant approaches focused at the nucleonic level, whether these be ab initio calculations, no-core shell model methods, large-basis shell model calculations, perhaps using Monte Carlo techniques, density functional theory (DFT) methods, or similar approaches. In these, the relevant degrees of freedom are those of the individual nucleons and the configurations they occupy. The interactions are those between/among nucleons. These approaches, long beset by the limitations of computing power, are enjoying a phenomenal renaissance in recent years due to stunning technological advances in computational ability. The hurdling of this barrier has itself inspired renewed interest in the above techniques leading to many important conceptual advances as well.

Nuclei are amazing systems. The intuitive picture of the nucleus as made up of up to hundreds of nucleons executing roughly 10²¹ orbits/sec and occupying some 60% of the total nuclear volume would lead one to expect utter chaos in the nucleonic motions. That this frequently does not occur, and that nuclei display striking regularities and simple patterns-of excitation energies, decay properties and transition matrix elements within a nucleus, and regular structural evolution over swaths of the nuclear chart-is largely a consequence stemming from the Pauli Principle. The orderly behavior frequently observed suggests that an alternate picture and approach may also give important insights and understanding. This alternate perspective consists of taking a few femto-steps back to look at the nucleus as a whole, and asking what kind of many-body symmetries, quantum numbers, collective coordinates and excitation modes, and decay selection rules it might exhibit.

Such an approach in fact predated the nucleonic description, with the ansatz of the liquid drop model, and flourished in the 1950s to the early 1980s with a sequence of models that had great successes. These models do not provide a priori predictions of nuclear properties, but correlate and explain, from a geometric perspective, a vast array of data, such as innumerable sequences of states that closely follow the eigenvalue expression for a rotating quantum mechanical symmetric top, multi-phonon states (levels with intact vibrational collectivity up through 5-phonon states have been seen in ¹¹⁰Cd), and evidence for other symmetries of motion and collective excitations. By far the most successful of them, in terms of parameter efficiency, flexibility to describe a rich variety of structures, the success of its predictions, and its revelations of new patterns of behavior and collective properties previously unrecognized, is the Interacting Boson Approximation (IBA) Model.

The ability of the IBA to correlate large amounts of data with, often, only two parameters (plus scale) presents an important challenge: if nucleon-based approaches can ultimately deduce the values of the parameters of the IBA, we will have, in effect, linked a femtoscopic approach to a vast array of data on collective behavior in nuclei. Attempts along these lines made initial progress in the early 1980s but ran into computational limits. However, these have now been overcome, and this is a topic well worth renewed interest.

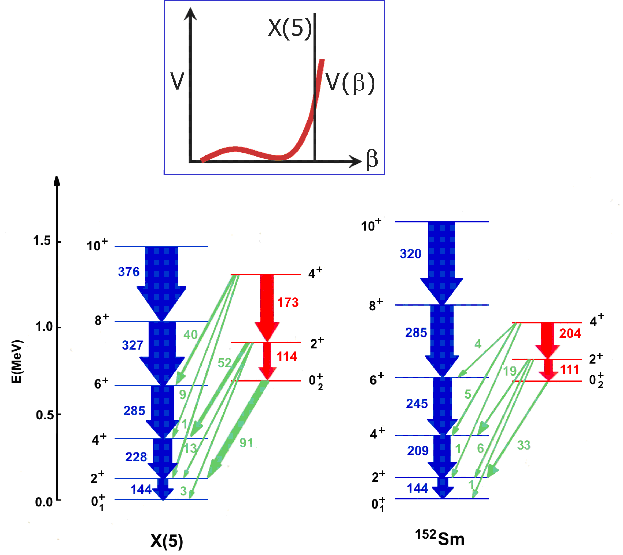
With the recent advances in computing capability in the last decade, the focus of interest in nuclear theory shifted and collective approaches fell into a period of the doldrums-until recently, with the discovery of behavior in certain regions of nuclei that resembles very much that of quantum (equilibrium or zero temperature) phase transitions (albeit muted due to the finite nature of the system). Nuclei at these shape/phase transitional points have historically been the most difficult to describe since they exhibit competing degrees of freedom associated with very different structures (e.g., spherical and axially deformed). However, they have recently been described by simple Critical Point Symmetries (CPS), based on a geometric description. As illustrated in the inset to Fig. 1, the key ansatz is simply that, at the phase transitional point, a square well is an excellent approximation to the collective potential as a function of the deformation "β". Two CPS, called E(5) and X(5), for transitions from spherical to γ-soft and axially symmetric deformed shapes, respectively, have been developed in the context of the Bohr Hamiltonian with an approximate separation of variables, and found to describe transitional nuclei remarkably well, in a parameter-free (except for scale) framework. The well-known comparison of X(5) with the data for ¹⁵²Sm is shown in Fig. 1.