Non-Equilibrium Quantum Field Theory:
Some answerable but unknown problems

Laurence G. Yaffe

Transport coefficients

How well can we compute transport coefficients in weakly coupled theories?

shear viscosity

(# denotes a known coefficient. See [Jeon] for the scalar case, and [Heiselberg] for the gauge theory case.) For gauge theories, leading-log results are useless for any practical application -- need complete dependence on . What is it? What are first sub-leading corrections suppressed by a power of coupling?

bulk viscosity

(See [Jeon].) What is leading parametric dependence on coupling for gauge theories? What is leading order result for gauge theories? What is next-to-leading order result for non-gauge theories?

electric conductivity

(See [Baym,Heiselberg].) What is complete leading-order dependence on ?

flavor diffusion

(See [Joyce, Prokopec, Turok].) What is complete leading-order dependence on ?

color conductivity

= Debye mass, = hard gluon damping rate. (See [Bodeker], and forthcoming paper by Arnold & Yaffe.) What is complete leading-order dependence on ?

Topological defect dynamics

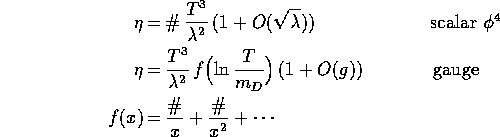
In equilibrium (at non-zero temperature) topological defects like monopoles will diffuse due to Brownian motion. What is the diffusion rate?

Domain (or bubble) walls (such as those separating hot and cold domains in a first order electroweak phase transion) experience ``frictional'' damping related by fluctuation-dissipation to their diffusion in equilibrium. For electroweak domain walls, the damping involves non-perturbative physics. What is the diffusion (or damping) rate?

Phase transition dynamics

In a (weakly coupled) theory with a second-order phase transition, cool from the hot to the cold phase by uniformly expanding the system at a fixed expansion rate .

small non-perturbative critical phenomena.

big complete perturbative control?

Can one reliably compute, for weak coupling and sufficiently large cooling rate, the complete time dependence of the effective temperature, the spatial correlation length, or the full probability distribution of long-wavelength fluctuations?

Effective field theories for

Static equilibrium observables

Imaginary time formulation

Euclidean QFT cutoff Euclidean QFT

Integrate out hard d.o.f. Sum of local operators in effective theory

Real time observables

High energy excitations can propagate for long times.
Suitable effective theories may have completely different forms:

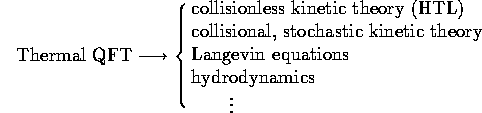
Fundamental weak coupling
long lived elementary excitations,
(appripriate) kinetic theory is leading order effective theory.

Can one systematically improve the leading order description?
N.B. Off-shell corrections are only suppressed by a power of g.
Must multiparticle correlations be included explicitly?
UV regularization of (most) real-time effective theories is highly non-trivial;
when are resulting theories well-defined & simulatable?

...answerable

Probably

...unknown

At least to me